Класифікація задач оптимізації

Для того, щоб повністю завдати рух об’єкта, необхідно знати його фазовий стан у початковий момент часу t₀ і вибрати керування u (t).

Цей вибір здійснюють за таких умов:

- задані крайові умови, тобто початковий y(t₀) і кінцевий y(t_к) стан об’єкта;

- оптимальність керування оцінюється за максимумом чи мінімумом функціоналу (10.3);

- на керування і змінні стану накладають обмеження (10.1);

Конкретизація всіх цих умов породжує різні типи задач оптимізації, які можна розділити на три групи за способом завдання:

- функціоналу І;

- обмежень;

- крайових умов.

Різні види функціоналу І були розглянуті вище.

За способом завдання обмежень задачі розділяють на:

- задачі з обмеженням на керування;

- задачі з обмеженням на фазові змінні;

- задачі зі спільним обмеженням на керування і на фазові змінні.

За способом завдання крайових умов задачі можна розділити на:

- задачі з фіксованими кінцями: задані значення y(t₀) і y(t_к), а також моменти часу t₀ і t_к;

- задачі з вільними кінцями: якщо y(t₀) чи y(t_к) не задані, то маємо задачу з вільним лівим чи правим кінцем відповідно;

- задачі з рухомими кінцями: у цьому випадку значення t₀ і t_к зафіксовані, а вектори стану y (t₀) і y (t_к) задані деякими множинами .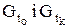

Крім зазначених ознак класифікації задач оптимізації, ці задачі можна розділяти за видом змінних і видом залежностей між ними.

За видом дії над змінними залежності можуть бути алгебраїчними і диференціальними. Задачі, що містять диференціальні залежності у функції часу, називають задачами динамічної оптимізації чи оптимального керування. Саме цим задачам приділяється основна увага у даній главі.

Дата добавления: 2014-01-07