Класичні методи варіаційного числення

Методи варіаційного числення можна умовно розділити на класичні й сучасні. До класичних належать методи, що ґрунтуються на рівняннях Ейлера, Лагранжа, Якобі, Вейєрштрасса. Їх доцільно застосовувати до задач, у яких області змін u (t) і y (t) не містять обмежень. Це має місце, коли розглядають малі відхилення u (t) і y (t) від усталених станів. Сучасні методи ґрунтуються на принципі максимуму Понтрягіна і методі динамічного програмування Беллмана. Їх перевагами є можливість урахування обмежень на керування та змінні стану, а також придатність до застосування ЕОМ.

Варіаційна задача з закріпленими граничними точками. Рівняння Ейлера

Під час вивчення перехідних процесів систем керування характер динаміки можна оцінювати величиною визначеного інтегралу. Наприклад, для одномірних об’єктів:

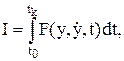(10.13)

де y = y(t), 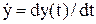- траєкторії координати виходу та її першої похідної за часом.

Технічна задача оптимізації динаміки об’єкта приводиться до математичної задачі знаходження екстремуму функціоналу (10.13). При цьому шукана функція повинна задовольняти крайовим умовам: y(t₀) = y₀; y(t_к) = y_k, де y₀, y_k – задані числа.

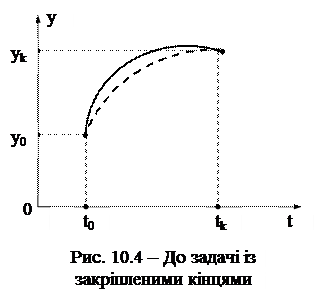
Така задача називається варіаційною задачею із закріпленими граничними точками (із закріпленими кінцями) (рис. 10.4).

Умова екстремуму інтегралу (10.13) при фіксованих граничних значеннях і відсутності обмежень на координати записується у вигляді рівняння Ейлера:

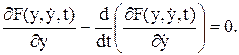(10.14)

Криві, на яких реалізується екстремум функціоналу (екстремалі), є інтегральними кривими цього рівняння. Для з’ясування, чи відповідає знайдена екстремаль мінімуму функціоналу, необхідно перевірити виконання додаткових умов. Оскільки це є достатньо складною процедурою, на практиці іноді обмежуються чисельною перевіркою значення функціоналу біля знайденої екстремалі.

Приклад 10.1 Знайти криву y^*(t), що проходить у фіксовані моменти часу t₀ і t_k через задані точки у₀ і у_k, на якій досягає екстремуму функціонал:

(10.15)

де k – задане число (k>0).

У даному випадк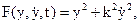у тому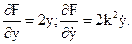

Рівняння Ейлера для екстремалей функціоналу (10.15) має вигляд:

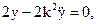або 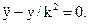(10.16)

Розв’язок цього рівняння запишемо у вигляді:

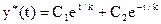. (10.17)

Для визначення С₁ і С₂ використовуємо граничні умови:

Тоді отримуємо:

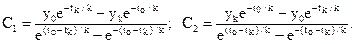(10.18)

У задачах оптимізації динаміки об’єктів у загальному випадку функціонал (10.13) може містити похідні вищих порядків. Необхідну умову наявності екстремуму такого функціоналу визначає рівняння Ейлера-Пуассона (за фіксованих граничних умов і відсутності обмежень на координати):

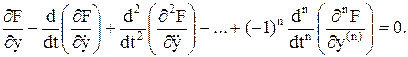(10.19)

Слід зазначити, що рівняння (10.14) і (10.19) застосовуються для знаходження екстремумів відповідних функціоналів тільки тоді, коли координати y(t) є безперервними гладкими функціями і не мають обмежень типу нерівностей.

Ці рівняння виражають першу необхідну умову екстремуму. Однак, залишається неясним, є отримані екстремалі максимумом чи мінімумом функціоналу. Відповідь на це запитання дає теорема Лежандра, яка виражає другу необхідну умову екстремуму:

Для того, щоб функціонал (10.13) у задачі із закріпленими кінцями досягав на кривій мінімуму (максимуму), необхідно, щоб уздовж цієї кривої виконувалась умова:

(10.20)

Так, для прикладу (10.1) маємо:

значить, на кривій (10.17) функціонал (10.15) досягає мінімуму.

Дата добавления: 2014-01-07