Геометрична інтерпретація оптимального керування

Вище було зазначено, що функції y_і є імпульсами і задають напрямок руху системи. Розглянемо розімкнуту систему керування об’єктом, що являє собою послідовне з’єднання двох аперіодичних ланок першого порядку (рис. 10.11). Запишемо рівняння ланок у нормальній формі Коші:

(10.67)

Функція Гамільтона матиме вигляд:

(10.68)

Спряжені рівняння мають вигляд:

(10.69)

Звідси знаходимо:

(10.70)

Для об’єкта, що розглядають, керування визначається вектором 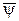, складова якого y₁ один раз змінює знак, а складова y₂ – знаку не змінює. Розглянемо оптимальне керування на фазовій площині (у₁; у₂) (рис. 10.12). Виходячи з початкових умов, припустимо, що перший інтервал є додатним, отже, і функції y₁ і y₂ також додатні, оскільки вони завдають напрямок розгону. Побудуємо на фазовій площині ділянку фазової траєкторії 1, що відповідає розгону. Вектор фазової швидкості буде направлений по дотичній до траєкторії зі складовими (10.67) Для досягнення максимуму функції Н необхідно, щоб знаки співпадали, тобто вектори - паралельні. У деякий момент часу функція y₁ змінює свій знак на від’ємний (10.70). Тому необхідно, щоб змінився знак і складової вектора фазової швидкості . Це можна зробити тільки за рахунок зміни знаку керуючої дії з + u на – u. При цьому рух буде відбуватися по траєкторії 2 (гальмування). Таким чином, і після зміни знаку вектори залишаються паралельними. Це й слугує ознакою оптимальності фазової траєкторії.

Дата добавления: 2014-01-07