Динаміка дискретних екстремальних систем

До цього типу належать крокові й кроково-імпульсні екстремальні системи. У останньому разі виконавчий механізм рухається не безперервно, а імпульсно, причому період слідування імпульсів Т₀ звичайно набагато більший за тривалість імпульсу t.

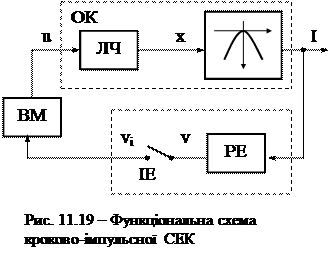
Розглянемо кроково-імпульсну систему (рис. 11.19). Рівняння ланок системи мають вигляд:

- об’єкт керування (ОК)

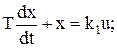(11.35)

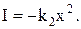(11.36)

- виконавчий механізм (ВМ)

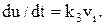(11.37)

- екстремальний регулятор (ЕР)

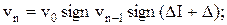(11.38)

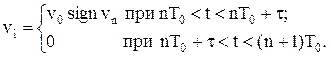(11.39)

Якщо v₀=const і t=const, то величина кроку при будь-якому n є постійною.

Характер руху кроково-імпульсної системи можна визначити методом фазової площини у координатах “вихідна величина І – її перша різниця DІ ”. Рівняння фазової траєкторії І = f(DІ) або, з урахуванням (11.36), х = f(Dх) можна визначити за допомогою z-перетворення.

У нашому випадку передавальна функція лінійної частини дорівнює:

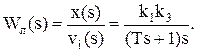(11.40)

Тоді імпульсна перехідна функція матиме вигляд (табл. 2.1):

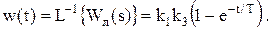(11.41)

Дискретна передавальна функція імпульсного фільтра, що розглядається, буде (табл. 8.1):

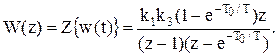(11.42)

З виходу релейного елемента знімається постійний сигнал 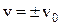, z-перетворення якого за умови 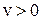має вигляд:

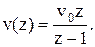(11.43)

Тоді z-перетворення вихідного сигналу х з урахуванням коефіцієнта передачі реального імпульсного елемента k_i=gТ₀, де g=t/Т₀ – відносна тривалість імпульсів, буде:

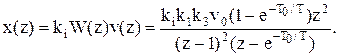(11.44)

Розкладемо (11.44) на прості дроби і позначимо: k_ik₁k₃v₀=k, 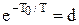. Тоді отримаємо:

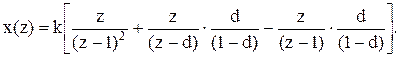(11.45)

З урахуванням властивості лінійності z-перетворення за допомогою оберненого z-перетворення отримаємо:

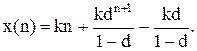(11.46)

Перша різниця Dх матиме вигляд:

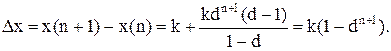(11.47)

Звідси: 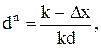або з урахуванням, що 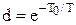, отримуємо:

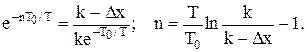(11.48)

Підставимо останній вираз до (11.46) і отримаємо рівняння фазової траєкторії х = f(Dx):

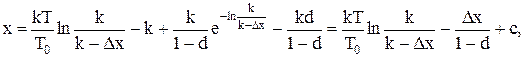
(11.49)

де с – стала, що враховує ненульові початкові умови х=х₀, Dх=Dх₀.

Тоді

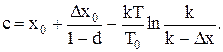(11.50)

Зазначимо, що при v<0 коефіцієнт k буде від’ємним, отже, знаки перед k у виразах (11.49) і (11.50) зміняться на протилежні. Для знаходження рівняння лінії перемикання, на якій відбувається змінювання знака величини v, використаємо рівняння регулятора (11.38).

Урахуємо, щ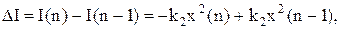о або

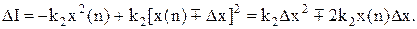(11.51)

З (11.38) видно, що змінювання знака v₀ має місце тільки при DІ+D = 0, тобто DІ = -D. Тоді з (11.51) отримаємо рівняння лінії перемикання на різницевій фазовій площині:

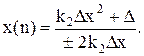(11.52)

Як і у разі безперервних екстремальних систем, у дискретних системах, що розраховані за допомогою різницевої фазової площини, важко встановити зв’язок між параметрами системи та її якістю. Тому для отримання заданих показників якості доводиться декілька разів виконувати розрахунки, змінюючи параметри екстремальної системи.

У закінченні зазначимо, що інерційність, що розташована до екстремального об’єкта (рис. 11.11, б), сповільнює рух системи до екстремальної точки, а інерційність, що розташована після об’єкта (рис. 11.11, в), сповільнює час вимірювання екстремуму, а отже, і визначення його положення.

Наведені вище аналітичні розрахунки СЕК базуються на достатньо повній інформації про об’єкт. Оскільки звичайно ця інформація є лише приблизною, остаточний висновок про доцільність застосування СЕК можна зробити лише після випробувань системи за промислових умов.

Дата добавления: 2014-01-07