Основные этапы применения факторного анализа в случае одного объясняющего фактора

В случае существования только одного фактора суть ФА состоит в объяснении корреляции между наблюдаемыми признаками с помощью корреляции этих признаков с фактором В общем случае может быть несколько факторов 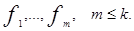Корреляцию между наблюдаемыми признаками и факторами обозначают 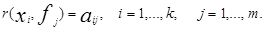Величины 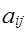называются факторными нагрузками и они образуют матрицу факторных нагрузок

Как правило, основная цель ФА состоит в объяснении корреляционной матрицы признаков R ее матрицей факторных нагрузок . Матрицу находят численными методами, определяя собственные числа и векторы матрицы Rприусловии выполнения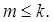

Предположим, существует один объясняющий фактор. На первом этапе формируют матрицу наблюдений (исходных данных),

Вычисленная корреляционная матрица матрицы наблюдений X равна:

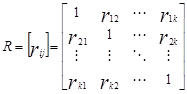
Целью факторного анализа является нахождение латентной переменной, так называемого фактора, который бы позволил воспроизвести наблюдаемую корреляционную матрицу с использованием соответствующей процедуры вычислений. Редуцированную (преобразованную) корреляционную матрицу 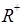можно воспроизвести с помощью вектора 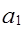факторной нагрузки по уравнению

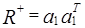(1)

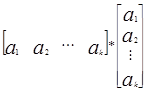или = (2)

Вектор представляет собой факторную нагрузку ненаблюдаемого фактора. В результате умножения 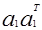получим матрицу 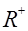, принципиально отличающуюся от диагональными элементами. Диагональные элементы матрицы 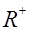называются общностями. Общность i- того элемента будем обозначать через 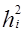. Величина 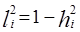называется характерностью. Диагональные элементы исходной и редуцированной корреляционных матриц связаны соотношением

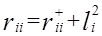(3)

Таким образом, значения компонент вектора , называемых факторными нагрузками, воспроизводят все коэффициенты корреляции для всех переменных. Фактор f непосредственно для измерения недоступен - он гипотетичен. Факторный анализ призван для установления таких гипотетичных факторов.

Из приведенного алгоритма ясно, что, прежде чем определить фактор, нужно построить редуцированную корреляционную матрицу по значениям общностей. Оценка общностей составляют первую проблему факторного анализа, проблему общности. Второй проблемой является определение фактора. Это так называемая проблема факторов.

Дата добавления: 2014-01-07