Системы координат. Системы отсчета

Все механические процессы происходят в пространстве и времени. Это находит отражение в любом механическом законе.

Положение тела в пространстве может быть определено только по отношению к другим телам. Тело отсчета – тело (система неподвижных тел), которое служит для определения положения интересующего нас тела.

Кроме тела отсчета нужна система, которая обеспечивала бы «адреса» других тел. С этой целью вводится система координат. Система координат позволяет определить положение тела в пространстве. Но нужна еще совокупность тела отсчета, связанных с ним координат и синхронизирующих часов – это система отсчета.

Заметим, что удачный выбор системы координат существенно облегчает решение задачи. Рассмотрим основные типы систем координат:

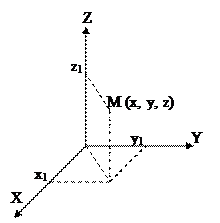1. Прямоугольная Декартова:

А) Двухмерная;

Б) Трехмерная;

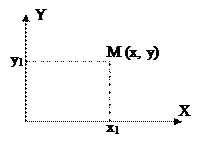
2. Цилиндрическая система координат:

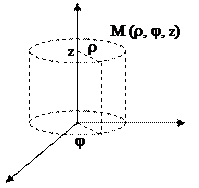
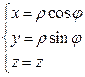
Задание: Найти координаты точки (1,1,1) в цилиндрической системе координат.

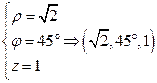
3. Сферическая система координат:

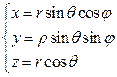
Задание: Найти координаты точки (1,1,1) в сферической системе координат.

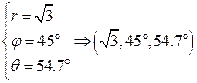
Формулы, связывающие координаты точки в одной системе отсчета с координатами в другой системе, называют формулами преобразования координат.

Скалярные, векторные величины. Действия над ними. Вычисление компонент вектора. Орты.

Для удобства координаты точки в любой системе координат будем обозначать одной буквой:

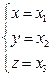
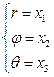
Вектор – направленный отрезок прямой, у которого один конец называется началом, а другой конец – концом. Модуль, направление, точка приложения, нулевой вектор.

Два вектора равны, если они имеют одинаковые модули и направление.

Противоположным вектору 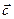называют вектор .

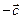Действия над векторами:

1. Сумма векторов:

a. Правило треугольника ;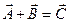

b. Правило прямоугольника;

Если при действии над векторами результат не изменяется при перестановке векторов, то говорят, что вектора обладают свойством коммутативности относительно этого действия.

2. Разность векторов 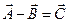или ;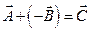

3. Умножение вектора на число ;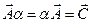

4. Скалярное произведение векторов:

Скалярным произведение векторов называют произведение модулей этих векторов на косинус угла между ними. Т.е. результат скалярного произведения – скаляр.

.

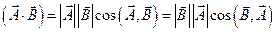Обладает свойством коммутативности.

Пример: .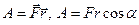

5. Векторное произведение:

В результате векторного произведения получается вектор, модуль которого равен произведению модулей перемножающихся векторов на синус угла между ними. Результирующий вектор направлен перпендикулярно плоскости перемножаемых векторов и направлен в сторону движения правого винта, если вращать его от первого вектора ко второму по кратчайшему пути.

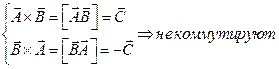
Модуль вектора C равен площади параллелограмма, построенного на A и B.

Компоненты векторных величин.

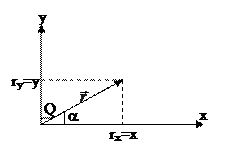
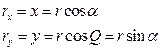
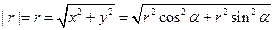
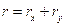
Орты:

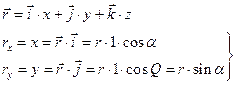
Скалярное и векторное произведение орт:

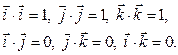
Скалярные произведения одноименных орт равны 1, разноименных – 0.

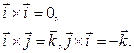
Векторное произведение одноименных орт равно 0. Модуль векторного произведения разноименных орт равен 1.

Действия над векторами в координатной форме.

Сумма векторов:

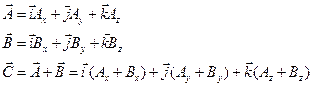
Компонент суммы двух векторов – сумма компонент слагаемых.

Скалярное произведение:

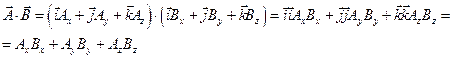
Векторное произведение:

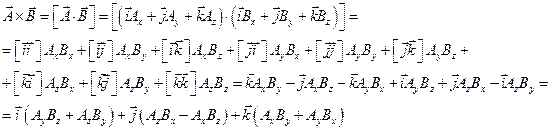
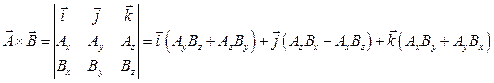
Радиус вектор – вектор, проведенный из начала координат в данную точку.

Перемещение и скорость в векторной и координатной формах.

Траектория – линия, вдоль которой движется тело.

Путь – расстояние вдоль траектории.

Перемещение – кратчайшее расстояние.

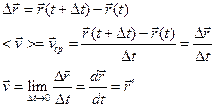
Вектором мгновенной скорости называют вектор, равный производной радиус-вектора по времени (направлен по касательной).

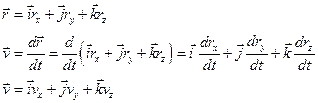
При прямолинейном движении .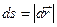

Абсолютное значение скорости (модуль):

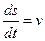
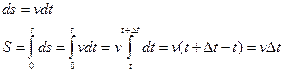
В общем случае при прямолинейном движении

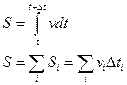
Если 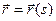, то через параметры траектории: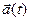

Ускорение в векторной и координатной формах.

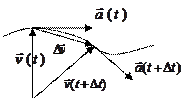
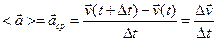
вектор среднего ускорения (скорость изменения скорости)

1.

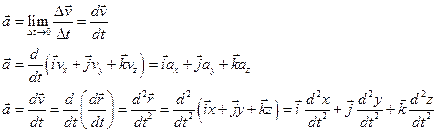
Вращательное движение:

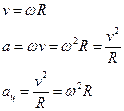
Изменение линейной скорости по направлению (меняется только направление).

Вектор ускорения – вторая производная вектора перемещения по времени.

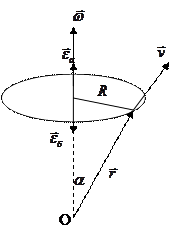
Кинематика вращательной точки. Угловая скорость.

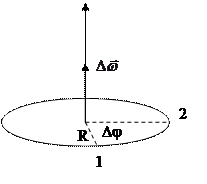
n – число оборотов.

Если w=const, то w - круговая (циклическая) частота.

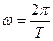
Т – период (время одного оборота).

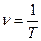- линейная частота.

Модуль 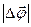равен углу поворота и направлен по оси вращения так, что направление поворота отвечает правилу винта.

- угловое ускорение.

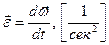
a) При равноускоренном движении вектор 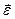направлен в ту же сторону что и .

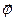b) При равнозамедленном – в обратную.

Вектора r, v и a называют естественными или полярными векторами.

Вектора 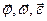- аксиальными.

Аксиальные вектора введены для объяснения физических процессов при вращательном движении. Они, так же как и полярные вектора подчиняются правилу сложения векторов.

Связь между линейными и угловыми величинами.

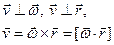, r – радиус-вектор.

По определению векторного произведения .

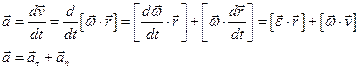
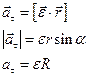
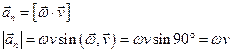
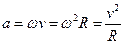
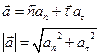
a_n=a_ц – изменение скорости по направлению за единицу времени.

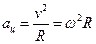
a_t – изменение скорости по модулю за единицу времени. При равномерном движении a_t=0.

Преобразование координат и компонент векторов.

Формулы, связывающие координаты точки в одной системе координат с координатами в другой называются преобразование координат.

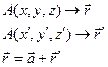
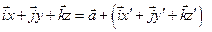
(1)

Для определения компоненты x умножим скалярно (1) на i:

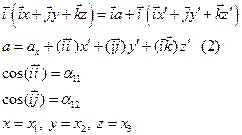
Тогда (2) запишем для случая a_x=0 (поворот):

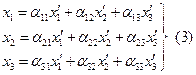
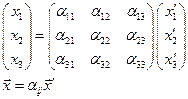
Пример: Преобразование координат для двухмерного случая.

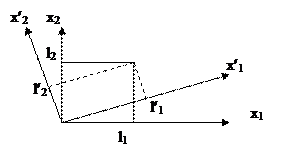
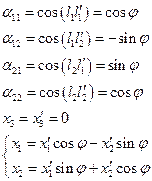
Значение скалярной величины определяется одним числом.

Значение вектора определяется тремя числами, которые называют компоненты вектора.

Более общее определение вектора:

Вектор – это упорядоченная совокупность трех чисел, зависящих от системы координат и преобразующихся при повороте системы отсчета так же, как преобразуются компоненты вектора.

При параллельном переносе компоненты вектора не изменяются:

Вектор тот же, но системы разные.

означает в координатной форме равенство компонент.

Величины, значения которых не изменяются при преобразованиях, называются инвариантами.

Вращение вокруг неподвижной оси.

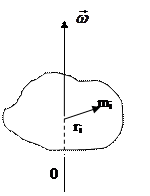
Для точки m_i имеем:

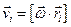
Рассмотрим момент импульса относительно оси 0. Общий момент импульса равен:

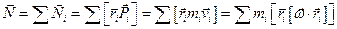
- двойное векторное произведение.

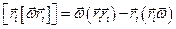
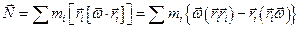
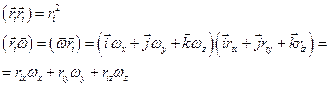
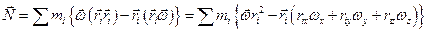
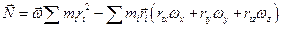
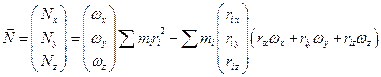
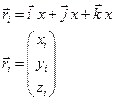
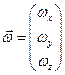
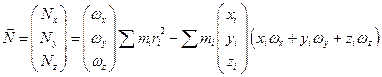
или

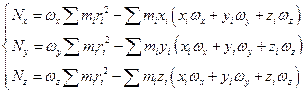
Запишем проекцию N_x:

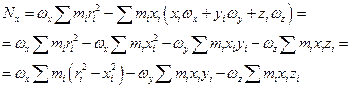
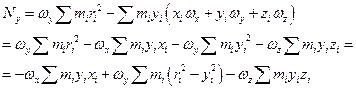
Аналогично преобразуем N_z .

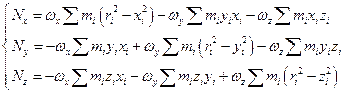
Введем инерциальные коэффициенты или моменты инерции:

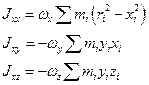
Имеем:

, , .

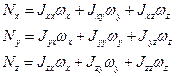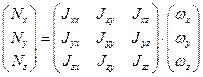Здесь обозначения аналогичные.

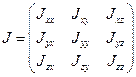
Совокупность величин образует тензор инерции.

Тензор симметричный, т.е. 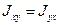и т.д. Таким образом тензор инерции определяется 6 числами.

Главные оси тензора инерции.

Симметричный тензор можно представить наглядно в виде эллипсоида, в данном случае эллипсоида инерции.

Тензор (второго ранга) – упорядоченная система 9 чисел, которые связывают два вектора.

Вектор (тензор первого ранга) – упорядоченная система трех чисел, которые преобразуются при изменении системы координат.

Скаляр (тензор нулевого ранга) – число, не изменяющееся при изменении системы координат.

Дата добавления: 2014-01-07