Приведение системы линейных уравнений к жордановой форме

Процесс отыскания решения системы линейных уравнений начинается с того, что система приводится к жордановой форме.

Определение. Жордановой формой системы (I.I) называется систе­ма линейных уравнений, обладающая следующими свойствами:

а) она равносильна системе (I.I)

б) в каждом уравнении жордановой формы есть такая переменная, которая входит в это уравнение с коэффициентом 1, а в остальные уравнения - с коэффициентом 0.

Так, если системе (I.I) равносильна следующая система линейных уравнений:

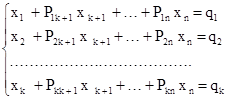(1.2)

то (І.2) есть жорданова форма для (I.I). При этом переменные х_1, х₂,...,х_к называются базисными, остальные переменные х_к+1,..., х_n называются свободными. Жорданова форма всегда является совместной системой линейных уравнений. Действительно, система (І.2) имеет следующее решение:

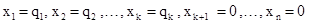(І.3)

Так как система (І.2) равносильна системе (І.І), то (І.3) является решением системы (І.І).

Таким образом, если для системы линейных уравнений (І.І) существует жорданова форма, то (І.І) – совместная система. Несовместная система жордановой формы не имеет.

Покажем, что любую совместную систему можно привести к жордановой форме. Это достигается методом Гаусса-Жордана, который состоит в следующем.

Рассмотрим первое уравнение системы (І.І). Выберем в нем переменную, коэффициент при которой отличен от нуля. Предположим, что а₁₁ ≠ 0. Поделим уравнение на а₁₁.

Получим уравнение

х₁+ а₁₂х₂ + … + а_1nх_n = в₁ (І.4)

Будем переменную х₁ делать базисной в жордановой форме. Для этого ее нужно исключить из остальных уравнений системы. Чтобы исключить х₁ из второго уравнения, умножим уравнение (І.4) на -а₂₁ и сложим со вторым уравнением. Затем исключим х₁ из третьего уравнения, для чего уравнение (І.4) умножим на –а₃₁ и сложим с третьим уравнением. Аналогично переменная х₁ исключается из остальных уравнений. Таким образом, взяв в качестве "ведущего" первое уравнение и проведя серию "жордановых исключений", мы получим равносильную (I.I) систему уравнений, вкоторой x₁ входит в первое уравнение с коэффициентом 1, а востальные уравнения - с коэффициентом 0.

После этого выбираем в качестве ведущего второе уравнение полученной системы. В этом уравнении берем коэффициент, отличный от нуля (пусть это коэффициент при х₂), делим уравнение на этот коэффициент и затем исключаем х₂ из всех остальных уравнений (в том числе и из первого). Затем в качестве ведущего выбираем третье уравнение и т.д.

Если на некотором шаге возникнет уравнение вида

0∙х₁ + 0∙х₂ +... + 0∙ х_n = 0 (І.5)

то удаляем его из системы. Если же возникнет уравнение вида

0∙х₁ + 0∙х₂ +... + 0∙ х_n = b ≠ 0, то это свидетельствует о несовместности исходной системы (І.І), а несовместная система к жордановой форме не приводится.

Таким образом, метод Гаусса-Жордана совместную систему линейных уравнений приводит к жордановой форме, а в случае несовместности системы обнаруживает несовместность.

Ясно, что вжордановой форме число уравнений не может быть больше числа уравнений в исходной системе. Так, если система (1.2) является жордановой формой для системы (I.I), то , причем строгое неравенство имеет место тогда, когда на некоторых шагах жордановой процедуры удалялись уравнения вида (1.5).

Очевидно, одна и та же система может иметь много различных жордановых форм.

Пример. Привести к жордановой форме

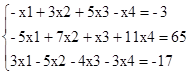
Выберем в качестве ведущего первое уравнение, а в качестве базисной переменной - переменную х_1. Поделим первое уравнение на (-1) (коэффициент при х₁), получим:

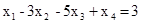
Умножим это уравнение на (+5) и прибавим ко второму уравнению, затем умножим его на (-3) и прибавим к третьему уравнению.

Получим систему:

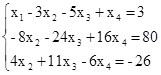
Теперь сделаем ведущим второе уравнение, а базисной переменной - переменную 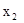. Поделив второе уравнение на (-8) и исключив 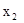из первого и третьего уравнений, получим систему:

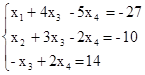
Наконец, в третьем уравнении выбираем в качестве базисной переменную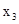. Поделим это уравнение на (-1) и исключим 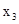из остальных уравнений. Получим жорданову форму:

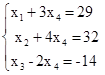
Переменные 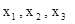являются базисными, переменная 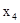- свободной.

Дата добавления: 2014-01-07