Условие оптимальности опорного плана

Табличный вид ЗЛП. Симплекс - таблицы.

СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗЛП

3.1. Общая характеристика и основные этапы симплекс – метода

Основоположниками симплекс-метода являются советский математик Л.В. Канторович и американский математик Дж. Данциг.

Симплекс-методом можно решить любую ЗЛП или обнаружить ее неразрешимость. Многие специальные классы ЗЛП можно решить другими, более эффективными для этих классов методами. Однако преимущество симплекс-метода - его универсальность. Почти для всех ЭВМ разработаны стандартные программы для решения ЗЛП симплекс - методом.

Опишем общую идею симплекс-метода.

Считаем, что ЗЛП записана в каноническом виде и целевую функцию нужно минимизировать. Как мы уже знаем, оптимальный план следует искать среди опорных планов ЗЛП. Симплекс-метод не перебирает все опорные планы (что было бы часто невозможно из-за их огромного количества), а, начиная с некоторого исходного опорного плана, он последовательно переходит к другим опорным планам с уменьшением целевой функции. Симплекс-метод прекращает свою работу тогда, когда либо будет найден оптимальный опорный план, либо установлена неразрешимость задачи.

При решении ЗЛП симплекс-методом можно выделить следующие этапы:

1) приведение ЗЛП к каноническому виду;

2) приведение системы линейных уравнений к жордановой форме с неотрицательными правыми частями с одновременной проверкой на неразрешимость ЗЛП из-за противоречивости системы линейных ограничений;

3) исследование опорного плана на оптимальность;

4) исследование ЗЛП на неразрешимость из-за неограниченности снизу на ОДР целевой функции;

5) переход к новому, "лучшему" опорному плану.

Для сокращения и упорядочения записей при решении ЗЛП симплекс-методом используются так называемые симплекс-таблицы. Чтобы воспользоваться симплекс-таблицей, ЗЛП нужно привести к табличному виду. Делается это так.

Пусть ЗЛП записана в каноническом виде (2.3-2.5). Для приведения ЗЛП к табличному виду систему (2.4) следует сначала привести к жордановой форме с неотрицательными правыми частями. Предположим, что эта жорданова форма имеет вид (2.6). Выразим из (2.6) базисные переменные через свободные:

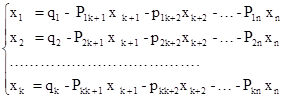(3.1)

Подставив в целевую функцию (2.3) вместо базисных переменных их выражения через свободные переменные по формулам (3.1), исключим тем самым из целевой функции базисные переменные. Целевая функция примет вид:

(3.2)

В табличном виде целевая функция записывается так:

(3.3)

где .

Отметим следующие особенности табличного вида ЗЛП:

а) система линейных уравнений приведена к жордановой форме с неотрицательными правыми частями;

б) из целевой функции исключены базисные переменные и она записана в форме (3.3).

Перейдем теперь к описанию симплекс-таблицы. Пусть ЗЛП записана в табличном виде:

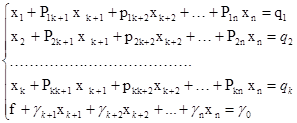(3.4)

Тогда заполненная симплекс-таблица выглядит так.

Таблица 3.1.

Базис	Переменные	Свободные члены
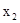
			...	xk			...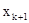
			...				...
			...				...
. . .	..	..	...	..	..	..	...	..	...
			...				...
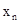
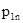
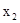
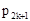
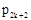
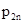
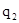
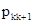
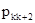
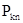
f			...				....

Опорный план ЗПЛ: 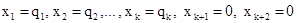..., называется опорным планом, соответствующим этой симплекс-таблице. Как видно из формулы (3.2), значение целевой функции при этом опорном плане равно γ₀.

Рассмотрим пример. Привести к табличному виду следующую ЗЛП и заполнить симплекс-таблицу:

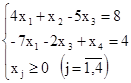
Вначале ЗЛП следует привести к каноническому виду. Для этого функцию f нужно заменить на - f:

Система уравнений должна быть записана в жордановой форме с неотрицательными правыми частями. Общий прием, с помощью которого это достигается, будет рассмотрен позднее (параграф 3.7). В нашем примере такая жорданова форма уже есть с базисными переменными 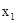и 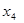. Исключим базисные переменные из целевой функции - f. Для этого выразим их через свободные и подставим эти выражения в целевую функцию.

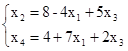
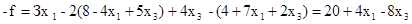
Табличный вид ЗЛП таков:

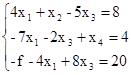
Заполним симплекс-таблицу (для сокращения записей первый столбец озаглавлен "Б", последний столбец - "Q").

Таблица 3.2.

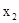
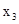
Б					Q
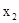
			-5
	-7		-2
-f	-4				-20

Опорный план, соответствующий этой симплекс-таблице, имеет вид:

. Значение функции - f при этом опорном плане равно - 20.

Пусть имеется заполненная симплекс-таблица. Сформулируем условие оптимальности опорного плана.

Если в нижней строке симплекс-таблицы все числа, кроме, быть может, самого правого, неположительны, то опорный план, соответствующий этой таблице, оптимален.

Для простоты обоснуем справедливость этого утверждения на примере. Пусть заполненная симплекс-таблица имеет вид:

Таблица 3.3.

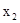
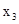
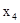
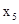
Б						Q
				-1
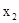
					-1
f			-5	-3	-1

Значение целевой функции при опорном плане, соответствующем симплекс-таблице, равно 6. Выпишем целевую функцию в табличном виде: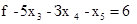, откуда . Так как при любом допустимом решении ЗЛП переменные принимают только неотрицательные значения, то из последней записи целевой функции видно, что ее значение в любой точке ОДР не меньше 6. Следовательно, минимальное значение целевой функции на ОДР равно 6 и оно достигается при опорном плане, соответствующем симплекс-таблице, .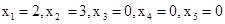

3.4. Условие неразрешимости ЗЛП из-за неограниченности снизу на ОДР целевой функции.

Если для ЗЛП заполнена симплекс-таблица, то ОДР задачи непуста, так опорный план, соответствующий симплекс-таблице, принадлежит ОДР. Однако ЗЛП может быть неразрешимой из-за неограниченности снизу на ОДР целевой функции.

Условие неразрешимости формулируется так.

Если симплекс-таблица содержит хотя бы один столбец, отличный от самого правого, у которого в нижней строке стоит положительное число, а во всех остальных строках столбца - неположительные числа, то ЗЛП неразрешима из-за неограниченности снизу на ОДР целевой функции.

Для обоснования снова воспользуемся примером.

Таблица 3.4.

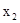
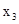
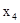
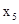
Б						Q
					-2
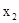
			-3		-1
f				-1

Столбец в нижней строке содержит положительное число, а в остальных строках - неположительные числа. Докажем неразрешимость ЗЛП.

Выпишем жорданову форму, соответствующую симплекс-таблице, и перенесем члены, содержащие 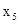, в правую часть. Получим

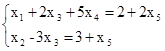
Пусть а - произвольное положительное число. Очевидно, ЗЛП имеет следующее допустимое решение: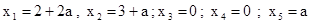. Вычислим значение целевой функции при этом допустимом решении. Из таблицы 3.4 имеем:

. При указанном допустимом решении f = 4 - 2а. Отсюда видим, что значение целевой функции может стать как угодно малым при достаточно большом значении а. Иначе говоря, целевая функция не ограничена снизу на ОДР. Следовательно, ЗЛП неразрешима.

3.5. Переход к новому опорному плану.

Предположим, что условия оптимальности и неразрешимости не выполняются. Тогда симплекс-метод переходит к новому опорному плану. Этот переход совершается за счет выведения из базиса одной из базисных переменных и введения в базис одной из свободных переменных. При этом должны выполняться следующие два условия:

1) новый базис должен быть по-прежнему допустимым, т.е. правые части соответствующей жордановой формы должны быть по-прежнему неотрицательными;

2) при новом опорном плане значение целевой функции не должно превышать ее значения при прежнем опорном плане.

Столбец симплекс-таблицы, в котором стоит переменная, вводимая в базис, называется генеральным столбцом. Строка, в которой стоит переменная, выводимая из базиса, называется генеральной строкой. Элемент, стоящий на пересечении генеральной строки и генерального столбца, называется генеральным элементом.

Правило выбора генерального элемента.

В качестве генерального столбца выбирается любой столбец симплекс-таблицы, отличный от самого правого, у которого в нижней строке стоит положительное число. Затем рассматриваются только те строки симплекс-таблицы, отличные от самой нижней, у которых на пересечении с генеральным столбцом стоят положительные числа. Для каждой из таких строк вычисляется отношение свободного члена к элементу, стоящему в генеральном столбце. Строка, для которой это отношение минимально, выбирается в качестве генеральной. Элемент, стоящий на пересечении генеральной строки и генерального столбца, и будет генеральным элементом.

Проиллюстрируем это правило на примере.

Таблица 3.5.

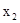
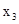
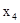
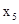
Б						Q
				2	-1
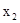
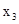
				-2
F

В качестве генерального столбца можно выбрать либо столбец 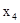, либо столбец 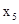. Выберем 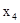(чаще всего выбирают тот столбец, у которого внизу большее положительное число). Теперь приступим к выбору генеральной строки. Для этого рассмотрим две строки - и 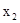. Составляем отношения 4:2 и 8:3. Меньшее значение имеет отношение 4:2, поэтому первую строку выбираем в качестве генеральной. Следовательно, генеральный элемент равен 2 - он стоит на пересечении столбца 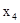и строки .

После выбора генерального элемента нужно перейти к новому опорному плану, при котором переменная становится базисной, а переменная х₁- свободной. Коэффициент при 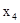в новой жордановой форме должен быть равен 1. Поэтому первая строка таблицы 3.5 делится на 2. Умножив затем полученную первую строку на (-3) и прибавив ко второй строке, исключим 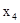из второго уравнения. Аналогично, с помощью жордановой процедуры исключаем 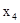из третьего уравнения и из целевой функции (последнее требует табличный вид ЗЛП).

В результате получим следующую таблицу.

Таблица 3.6

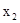
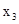
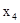
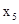
Б						Q
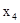
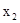
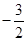
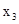
f		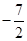				-2

Обратим внимание, что в столбце Q в первых трех строках стоят неотрицательные числа, т.е. новый базис 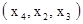по-прежнему является допустимым. Это не случайный факт: так будет всегда при точном соблюдении правила выбора генеральной строки. Далее, значение целевой функции при новом опорном плане равно -2, при старом оно было равно 12. "Улучшение" опорного плана гарантирует правило выбора генерального столбца. Хотя эти факты мы строго не доказываем, следует иметь в виду, что они всегда имеют место.

Посмотрев на таблицу З.6, мы видим, что не выполняются ни условие оптимальности опорного плана, ни условие неразрешимости ЗЛП. Значит, надо снова выбирать генеральный элемент и переходить к новой симплекс-таблице. Читатель сможет проделать это самостоятельно.

3.6. Табличный симплекс-алгоритм.

Пусть имеется заполненная симплекс-таблица. Подводя итоги изложенному, получим следующий алгоритм решения ЗЛП симплекс-методом.

1. Если в нижней строке симплекс-таблицы все числа, кроме, быть может, самого правого, неположительны, то опорный план, соответствующий симплекс-таблице, оптимален, и алгоритм останавливается. В противном случае - переход пункту 2.

2. Если симплекс-таблица содержит столбец, отличный от самого правого, у которого в нижней строке стоит положительное число, а во всех остальных строках - неположительные числа, то ЗЛП неразрешима из-за неограниченности снизу на ОДР целевой функции, и алгоритм останавливается. В противном случае - переход к пункту 3.

3. Выбираем любой столбец, отличный от самого правого, у которого в нижней строке стоит положительное число - назовем его генеральным. Затем рассматриваем строки симплекс-таблицы, отличные от самой нижней, у которых в генеральном столбце стоят положительные числа. Для каждой из таких строк вычисляем отношение свободного члена к элементу, стоящему в генеральном столбце. Строка, для которой это отношение минимально, является генеральной строкой. Элемент, стоящий на пересечении генерального столбца и генеральной строки, будет генеральным элементом. Переход к пункту 4.

4. Составляем новую симплекс-таблицу, в которой:

1) из базиса выведена переменная, стоящая в генеральной строке; в базис введена переменная, стоящая в генеральном столбце;

2) генеральная строка поделена на генеральный элемент;

3) с помощью жордановой процедуры все числа генерального столбца, за исключением 1, стоящей в генеральной строке, делаются равными нулю. Переход к пункту 1.

Пример I. Решить симплекс-методом

Задача записана в каноническом виде, нужно привести ее к табличному виду. Система уравнений записана в жордановой форме с неотрицательными правыми частями (базисные переменные и 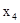). Необходимо привести к табличному виду целевую функцию. Для этого выразим базисные переменные через свободные

x₃=10 - 2x₁ - x₂

x₄= 8 - x₁ - 2x₂

и подставим в целевую функцию

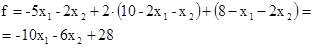
Для получения табличного вида функцию запишем так:

Теперь имеем табличный вид ЗЛП:

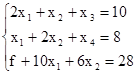
Заполним первую симплекс-таблицу

Таблица 3.7

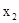
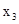
Б					Q
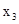
F

В таблице 3.7 условия оптимальности и неразрешимости не выполняются. Выберем в качестве генерального столбец , у которого в нижней строке стоит положительное число. Затем, сравнивая отношения 10:3 и 8:1, выберем первую строку в качестве генеральной. В таблице генеральный элемент 2.

Действуя в соответствии с пунктом 4 табличного симплекс-алгоритма, перейдем к таблице 3.8.

Таблица 3.8

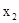
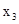
Б					Q
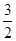
F			-5		-22

Условия оптимальности и неразрешимости не выполняются. Выбираем в таблице 3.8 генеральный элемент и переходим к следующей таблице

Таблица 3.9

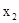
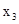
Б					Q
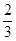
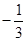
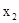
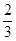
F		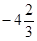			-24

Таблица 3.9 удовлетворяет условию оптимальности.

Ответ: оптимальный план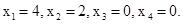

Минимальное значение целевой функции f_min = - 24.

Пример 2. Решить симплекс-методом:

Прежде всего, ЗЛП нужно привести к каноническому виду

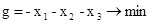
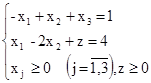
Теперь приводим ЗЛП к табличному виду. Видим, что система уравнений записана в жордановой форме с неотрицательными правыми частями (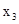и z- базисные переменные). Однако в целевую функцию входит базисная переменная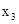. Имеем:

Следовательно, табличный вид ЗЛП таков:

Заполняем симплекс-таблицу (таблица 3.10).

Таблица 3.10

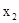
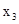
Б				z	Q
	-1
z		-2
g					-1

После выбора генерального элемента переходим к таблице 3.11

Таблица 3.11

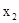
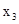
Б				z	Q
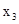
		-1
z		-2
g				-2	-9

Обратим внимание на столбец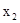. Он показывает, что целевая функция g не ограничена снизу на ОДР. Вспоминая, что g =-f, получаем ответ.

Ответ: ЗЛП неразрешима из-за неограниченности сверху на ОДР целевой функции f.

Пример 3. Решим симплекс-методом задачу об использовании оборудования, поставленную в параграфе 2.1. Там же приводилась ее математическая модель

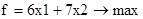
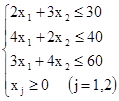
Приводим ЗЛП к каноническому виду

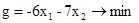
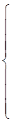
Система уравнений записана в жордановой форме с неотрицательными правыми частями, базисные переменные 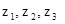не входят в целевую функцию g. Поэтому табличный вид целевой функции таков:.

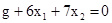Заполняем симплекс-таблицу (таблица 3.12).

Таблица 3.12

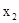
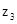
Б						Q
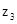
G

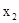Условия оптимальности и неразрешимости не выполняются. Столбец (в нижней строке которого стоит наибольшее положительное число) выберем в качестве генерального. Сравнивая отношения 30:3, 40:2, и 60:4, объявляем генеральной первую строку. Поделив ее на 3 и сделав с помощью жордановой процедуры нули во всех остальных строках генерального столбца, после замены базисной переменной на переменную , получим таблицу 3.13.

Таблица 3.13

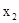
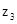
Б						Q
x2
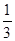
z2
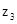
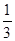
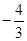
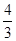
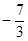
g						-70

Снова выбираем генеральный элемент и переходим к таблице 3.14

Таблица 3.14

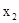
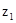
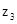
Б						Q
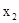
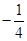
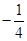
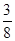
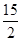
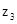
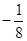
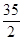
g			- 2		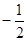	-80

В нижней строке таблицы 3.14 стоят неположительные числа. Поэтому опорный план, соответствующий этой таблице, оптимален. Выпишем его:

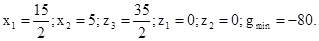
Так как переменные 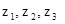не фигурировали в исходной постановке задачи, кроме того, функция f = - g в исходной постановке максимизировалась, то можно записать следующее оптимальное решение исходной задачи

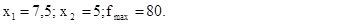
Возвращаясь к содержательной постановке (параграф 2.1), получаем следующий вывод: прибыль предприятия будет максимальной (равной 80 ден.ед.), если изделий А выпустить 7,5 ед., изделий В выпустить 5 ед.

Эту же задачу мы решили геометрически (см. параграф 2.5, пример 5) и, естественно, получили тот же результат.

Дата добавления: 2014-01-07