Решение ЗЦЛП методом округления

Целочисленная задача об использовании сырья.

Предприятие выпускает n видов штучной продукции стоимостью 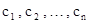за штуку. Для изготовления продукции используется m видов сырья, запасы которого на предприятии равны соответственно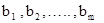. Известна (m X n) – матрица (a_ij), в которой 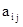- расход i – го сырья на производство единицы продукции j –го вида. Требуется составить такой план производства, при котором выручка от реализации продукции была бы наибольшей.

Математическая модель задачи имеет вид:

f =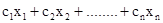→ max

при ограничениях:

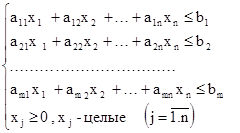
Здесь 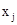- количество продукции j –го вида.

Это задача целочисленного линейного программирования.

Целочисленность переменных существенна в тех случаях, когда речь идет о производстве дорогостоящей продукции.

6.3. Задача о рюкзаке.

Целочисленная задача об использовании сырья не является ярко выраженной ЗЦЛП. К типичным ЗЦЛП относятся т.н. комбинаторные оптимизационные задачи. В комбинаторных задачах имеется конечное множество вариантов, из которых нужно выбрать оптимальный. Примером такой задачи является задача о рюкзаке.

Имеется рюкзак вместимостью V и n предметов объемами v₁, v₂,...,v_n и стоимостями с₁, c₂ ,..., c _n. Требуется упаковать рюкзак так, чтобы стоимость упакованных предметов была максимальной.

Составим математическую модель этой задачи.

Пусть x_j – переменная, принимающая только два значения: 0 или 1, причем x_j =0, если j-й предмет не упаковывается в рюкзак; x_j = 1, если j-й предмет упаковывается в рюкзак. Тогда задача записывается так:

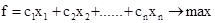
при ограничениях

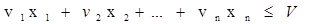
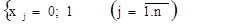
Это ЗЦЛП, называемая задачей булева программирования. Ограничения задачи можно записать иначе:

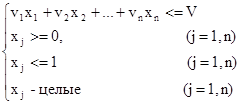
Метод округления – простейший метод приближенного решения ЗЦЛП. Его сущность состоит в том, что решается ослабленная задача (как задача линейного программирования) и полученное оптимальное решение ЗЛП округляется до целочисленного решения. Этот метод имеет два существенных недостатка:

1) в результате округления может получиться недопустимое решение;

2) решение, полученное в результате округления, являясь допустимым, может значительно отличаться от оптимального.

Пример 1.

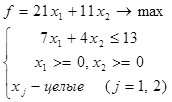
Решив геометрически ослабленную задачу, получаем оптимальное решение:

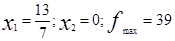
Произведем округления:

1) x₁=2; x₂=0. Получим недопустимое решение - не удовлетворяется ограничение 7x₁+4x₂<=13 (действительно, 7*2+4*0<=13 – ложное неравенство).

2)х₁=1; х₂=0. Это допустимое решение. Значение целевой функции f=21*1+11*0=21, что сильно отличается от оптимального значения.

Оптимальное решение этой ЗЦЛП таково: х₁=0; х₂=3; f_max =33.

Метод округления можно использовать тогда, когда целевая функция малочувствительна к изменениям переменных в пределах единицы.

Дата добавления: 2014-01-07