Теорема 1 (существования и единственности решения задачи Коши)

Пусть функция 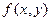и ее частная производная 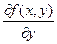непрерывны в некоторой области 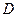на плоскости 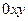, и точка 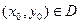. Тогда задачи Коши (13.4) имеет решение и притом единственное. Это решение определено в некоторой окрестности точки .

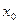Доказательство этой теоремы достаточно сложно и требует введения ряда дополнительных понятий, поэтому мы оставим его за пределами данных лекций.

Геометрический смысл теоремы заключается в том, что через точку 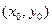проходит единственная интегральная кривая.

Определение 4. Пусть в области 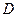выполняются условия теоремы 1. Функция

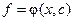, (5)

где 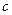– постоянная, называется общим решением уравнения первого порядка (3) в некоторой окрестности точки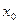 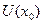, если:

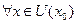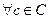1. При и , где 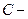некоторое множество (в простых случаях 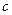вообще любое) функция (5) является решением уравнения (3).

2. Для любого начального условия 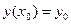, где 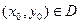, существует значение постоянной 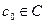, при котором функция (5) удовлетворяет этому начальному условию: .

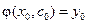Определение 5. Равенство вида 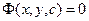, неявно задающее общее решение, называется общим интегралом дифференциального уравнения первого порядка (3).

Некоторые типы дифференциальных уравнений первого порядка

и методы их решений

В этом параграфе будут рассмотрены некоторые уравнения вида 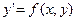и указаны методы решения таких уравнений 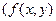будет предполагаться удовлетворяющей условиям теоремы 1).

Уравнения с разделяющимися переменными это уравнения вида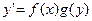или

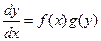. (6)

Решение. Предполагая, что 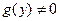, запишем последнее равенство в виде 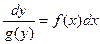(таким образом, мы сумели «разделить переменные» в уравнении (6)). Считая, что 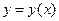есть решение исходного уравнения, мы видим, что последнее равенство есть равенство дифференциалов двух функций от 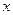, которое может выполняться тогда и только тогда, когда сами эти функции, или интегралы от их дифференциалов, отличаются на произвольную постоянную: 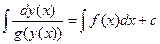, или

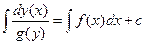. (7)

Равенство (7), имеющее вид 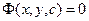, является общим интегралом исходного дифференциального уравнения (6).

Пример. Решить дифференциальное уравнение .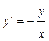

Решение.

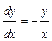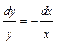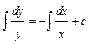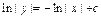; ; ; . Из полученного равенства вида (7) в этом примере можно выразить 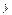. Заменяя 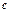на 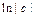(то и другое – произвольные постоянные), имеем:

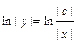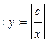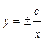; ; ; , или (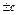можно заменить на ) .

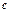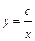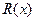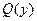После деления на и переменные разделяются также в уравнениях вида

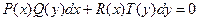: (8)

.

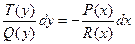Уравнения, сводящиеся к уравнениям с разделяющимися переменными:

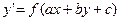, (9)

где 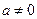, , 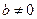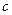– некоторые постоянные.

Решение. Сделаем в уравнении (9) замену 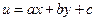, где 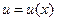– новая неизвестная функция. Тогда 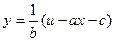, , 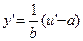и (9) принимает вид 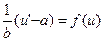; ;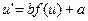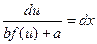, т.е. переменные разделились.

Пример. Решить дифференциальное уравнение .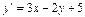

Решение.

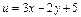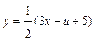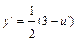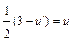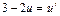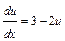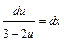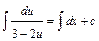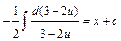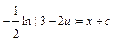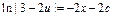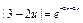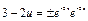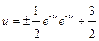; ; ; ; ; ; ; ; ; ; ; ; ; ; заменяя здесь 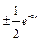на 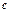, имеем: 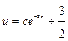, откуда

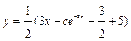
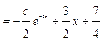, или, заменяя 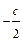на , .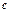

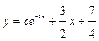Однородные уравнения первого порядка это уравнения вида

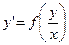(10)

(т.е. в этих уравнениях правая часть зависит только от отношения ).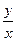

Решение. Сделаем в уравнении замену 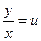, где 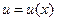– новая неизвестная функция: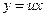; 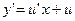. Тогда уравнение примет вид 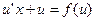, или 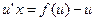. Но последнее уравнение является уравнением с разделяющимися переменными: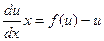; 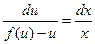и решается как все такие уравнения: .

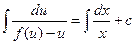Пример. Решить дифференциальное уравнение .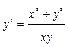

Решение.

Переписав это уравнение в виде 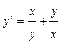, мы видим, что оно является однородным. После замены 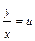, 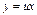; 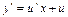, уравнение примет вид 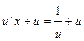; 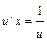. Разделяем переменные в последнем уравнении: 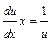; 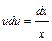. Далее имеем:; ; ; ; ; ; .

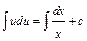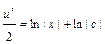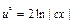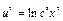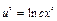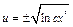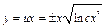Уравнения, сводящиеся к однородным:

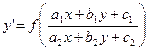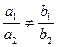, . (11)

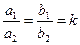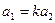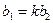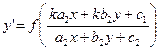
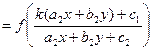
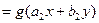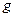Заметим, что если , то , , и (11) примет вид , где – некоторая функция, т.е. вид (9), и будет решаться как уравнение такого вида.

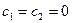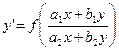
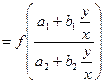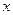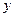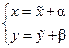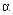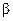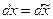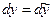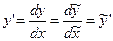Если бы в уравнении (11) , то это уравнение имело бы вид , т.е. вид (10), и являлось бы однородным. Поэтому мы будем пытаться путем некоторой замены (аргумента и искомой функции ) обратить эти коэффициенты в 0. Положим , где и – некоторые числа. Тогда , и , где 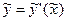. Уравнение (11) теперь принимает вид

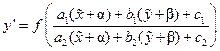
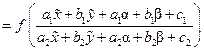. Теперь подберем

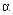и 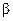так, чтобы 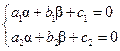. Эта система имеет единственное решение, так как ее определитель 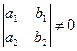, ибо, по условию, строки этого определителя не пропорциональны. При таких 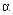и 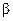наше уравнение, как было показано выше, становится однородным.

Пример. Решить дифференциальное уравнение .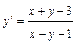

Решение.

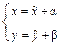
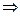
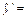
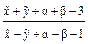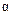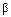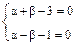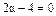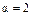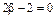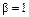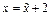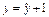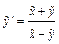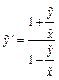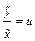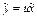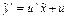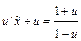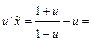
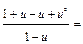
; и должны удовлетворять системе; складывая и вычитая уравнения, имеем: , ; , ; т.е. , ; при такой замене ; ; в последнем однородном уравнении сделаем замену , , ; тогда ; ; 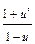разделяем переменные: 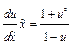; ; 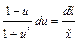интегрируем: ; ;

; ;

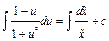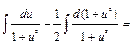
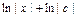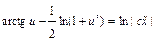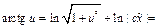
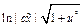теперь вернемся к переменным 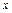и 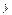; подставляя в эту формулу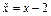 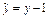, , 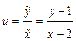имеем:

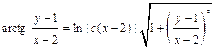, или ;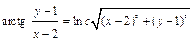

последнее равенство есть общий интеграл исходного дифференциального уравнения.

Линейные уравнения первого порядка это уравнения вида

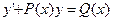. (12)

Существуют два метода решения линейных уравнений, которые отличаются друг от друга лишь формой записи.

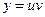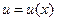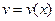Первый способ (метод Бернулли). Будем искать решение уравнения (12) в виде , где , – некоторые функции. Тогда 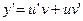и (12) принимает вид 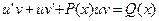. Перепишем последнюю формулу следующим образом:

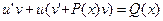(13)

Теперь выберем функцию 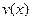такой, чтобы

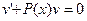, (14)

а затем найдем все функции 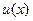, при которых справедливо равенство (13) (т.е. при нахождении решения в виде произведения двух сомножителей мы выбираем один из этих сомножителей как нам удобно, а затем находим второй сомножитель так, чтобы их произведение было решением).

Разделяя переменные, имеем:

; ; ; ;

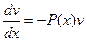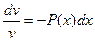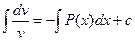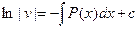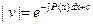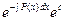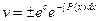=; , или .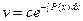

Так как нам достаточно найти лишь одно решение уравнения (13.14), то возьмем в последней формуле 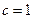, и тогда

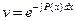. (15)

Далее из (13) и (15) имеем: ; ;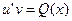

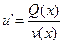
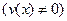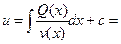
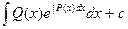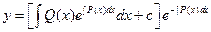; (16)

Эта функция и есть общее решение исходного линейного уравнения (12).

Пример. Решить дифференциальное уравнение .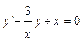

Решение.

Обычно в примерах не используют готовую формулу (13.16), а проводят для каждого конкретного уравнения те действия, которые к ней привели. Будем искать решение уравнения в виде 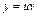. Тогда 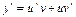, и уравнение принимает вид 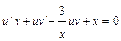; 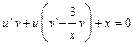. Потребуем, чтобы 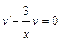, тогда 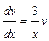; ; 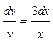;; 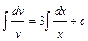; ;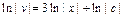 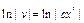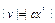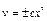, или 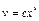. Принимая здесь 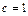, получаем, что 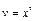. Теперь 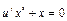; ; 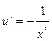отсюда 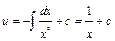, и .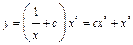

Второй способ (метод вариации произвольной постоянной). Рассмотрим так называемое линейное однородное уравнение, соответствующее данному уравнению (13.12):

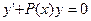. (17)

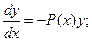
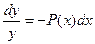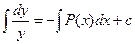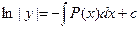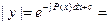
Решаем это уравнение (с разделяющимися переменным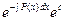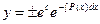и):; ; ;; , или

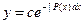. (18)

Теперь будем искать решение уравнения (12) по той же формуле (18), считая, что в ней 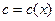(отсюда и название метода). Тогда

=.

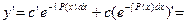
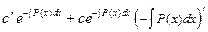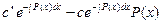Подставляя эту производную в (12), имеем:

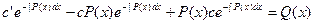, или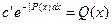

(т.е. члены с 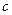всегда сокращаются, остается только член с ).

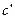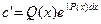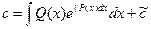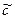Отсюда ; , и (заменяем на 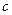) 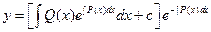, т.е. мы опять получили формулу (16).

Пример. Решить задачу Коши .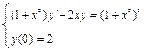

Решение.

Переписав это уравнение в виде 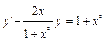, мы видим, что оно действительно является линейным. Соответствующее однородное уравнение имеет вид 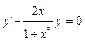. Решаем это уравнение: ; ; ; ;

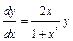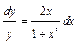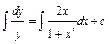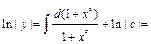
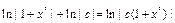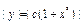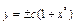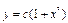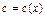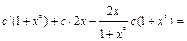
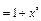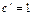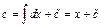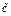; , или . Теперь ищем решение исходного уравнения по этой же формуле, считая, что в ней . Подставляя в уравнение, имеем: ; ; , и (заменяем на 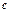) 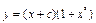. Подставляя сюда х = 0, имеем:

2 = с, т.е. единственное решение задачи Коши имеет вид .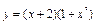

Уравнения Бернулли это уравнения вида

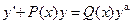, (19)

где 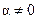, 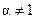(при 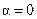получаем линейное уравнение, а при 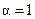– уравнение с разделяющимися переменными).

Легко убедиться, что к уравнениям Бернулли применим любой из описанных выше методов решения линейных уравнений.

Пример. Решить дифференциальное уравнение .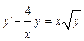

Решение.

1-й способ: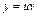; ; 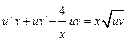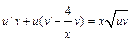. Потребуем, чтобы 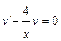, тогда 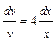; ; 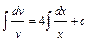;; 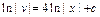; ;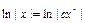 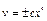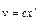при .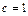

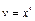Тогда ; ; ; ;; ; .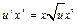

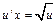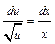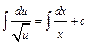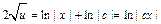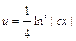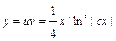2-й способ: Решаем соответствующее однородное уравнение 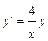. Имеем: 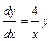; ; 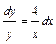; ; 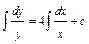;; 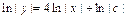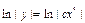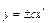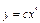. Теперь ищем решение исходного уравнения по этой формуле, считая, что в ней 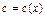. Подставляя в уравнение, имеем: ; ; ; ; ; ; .

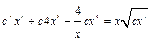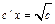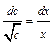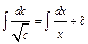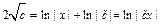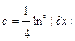Уравнения в полных дифференциалах это уравнение вида

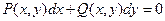(20)

в котором левая часть является (полным) дифференциалом некоторой функции двух переменных, т.е. существует функция 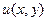, такая, что .

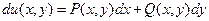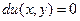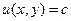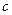В этом случае уравнение (20) имеет вид , что выполняется в том и только в том случае, когда , где – некоторая (произвольная) постоянная. Последнее равенство является общим интегралом уравнения (20).

Ранее была изложена

Теорема 2. Пусть функци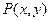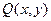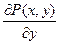и , , и 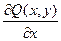непрерывны в области 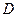. Тогда для того, чтобы в D выражение 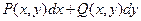являлось полным дифференциалом некоторой функции двух переменных, необходимо, а в предположении односвязности области и достаточно, чтобы при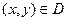

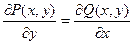(21)

и приведены формулы для нахождения функции :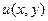

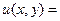
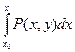
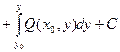(22)

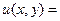
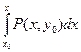
и 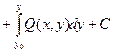. (23)

Пример. Решить дифференциальное уравнение .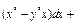

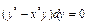Решение.

В этом примере 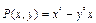, 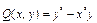непрерывны вместе со своими частными производными на всей плоскости 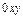. 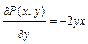, , 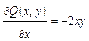т.е.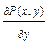 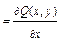, значит, уравнение является уравнением в полных дифференциалах (кстати, отметим, что оно также является однородным). Взяв 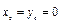, из формулы (22) имеем (достаточно знать одну функцию 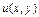, поэтому берем ): .

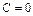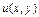
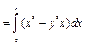
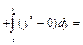
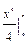
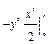
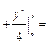
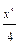
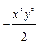
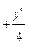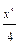
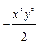
Общий интеграл уравнения имеет вид 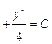, или .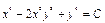

Дифференциальные уравнения высшихпорядков

Дифференциальное уравнение n -го порядка имеет вид 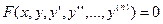. Если из этого уравнения можно выразить старшую производную 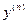, то мы получим так называемое уравнение, разрешенное относительно старшей производной (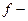некоторая функция 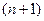-й переменной).

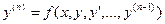. (24)

Определение 6. Задачей Коши для уравнения (24) называется задача

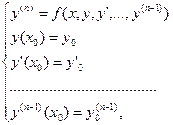(25)

где 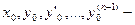некоторые числа.

Теорема 3 (существования и единственности решения задачи Коши) (без доказательства). Пусть функция 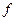и ее частные производные первого порядка по всем аргументам, кроме 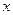, непрерывны в некоторой области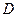 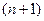- мерного пространства и точка 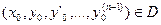. Тогда задача Коши (25) имеет единственное решение (определенное в некоторой окрестности точки ).

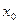Определение 7. Пусть выполняются условия теоремы 3. Функция

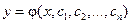, (26)

где 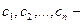постоянные, называется общим решением уравнения (24) в некоторой окрестности точки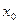 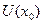, если:

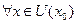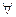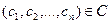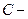1. При и наборе , где некоторое множество (в простых случаях 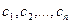, будут любыми числами) функция (26) является решением уравнения (24).

2. Какие бы начальные условия 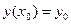,,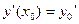…, , 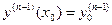где точка 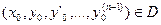, мы не задали, существует набор 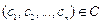, при котором функция (26) удовлетворяет этим начальным условиям.

Определение 8. Равенство вида 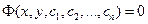, неявно задающее общее решение, называется общим интегралом уравнения (24).

Уравнения, допускающие понижение порядка

Одним из методов решения дифференциальных уравнений высших порядков является сведение их к уравнениям меньшего (лучше первого) порядка. Рассмотрим два основных типа уравнений, допускающих понижение порядка.

1. Уравнение не содержит явным образом искомую функцию y и, может быть, несколько ее первых производных, т.е. имеет вид

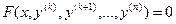. (27)

Сделаем в этом уравнении замену 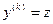, где 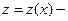новая неизвестная функция (т.е. за новую неизвестную функцию берется производная наименьшего порядка, входящая в это уравнение). Тогда 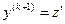, , 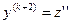…, , 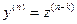и (27) примет вид 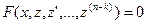, и порядок уравнения понизился.

Пример. Решить задачу Коши для дифференциального уравнения .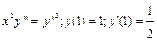

Решение.

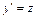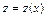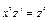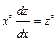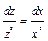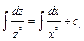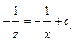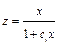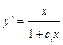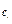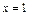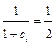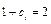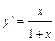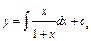
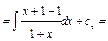
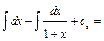
Обозначая , , имеем . Это уравнение первого порядка является уравнением с разделяющимися переменными:; . Интегрируя, получаем: ; ;; , т.е. . Прежде чем интегрировать еще раз, найдем из второго начального условия. При из него ; ; . Значит .Отсюда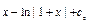. Подставляя 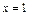, из первого начального условия находим постоянную 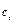: 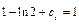; 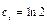. Таким образом, .

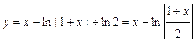Если бы нам нужно было найти общее решение исходного уравнения, то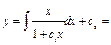

=.

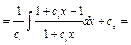
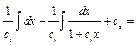
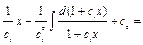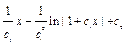2. Уравнение не содержит явным образом независимую переменную х, т.е. имеет вид

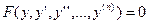. (28)

Сделаем в этом уравнении замену 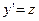, где 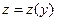, т.е. за новую независимую переменную мы берем 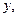а за новую независимую функцию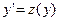. Покажем, что при такой замене порядок уравнения понижается на единицу:

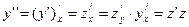, т.е. ,

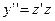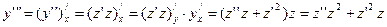
и так далее, т.е. порядок каждой производной становится на единицу меньше.

Пример. Решить дифференциальное уравнение .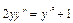

Решение.

Обозначая 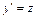, , 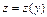, 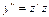имеем 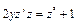. Это уравнение первого порядка, опять-таки, является уравнением с разделяющимися переменными: 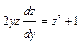; 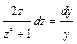. Интегрируя, получаем: 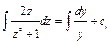; ;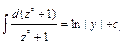; ;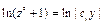 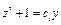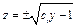, т.е. 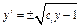. Еще раз разделяем переменные: 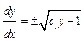; 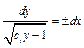. Далее имеем: 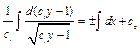; 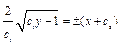. Возводя в квадрат обе части, находим общее решение :

; ; .

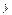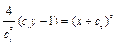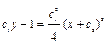Если бы мы решали задачу Коши для нашего уравнения, т.е. добавили бы к нему начальные условия, например, 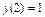, , 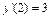то постоянные тоже проще было бы находить «по дороге»: считая, что в равенстве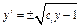 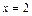, получаем: 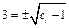; значит, знак нужно брать «+» и , ;

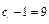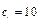тогда, аналогично изложенному выше, 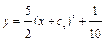и при 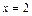отсюда 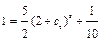; ; 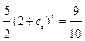; ; 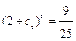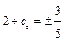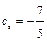или .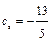

Дата добавления: 2014-01-07