Матричные методы определения кратчайших путей

Метод, предложенный Шимбелом [], предусматривает определение величины кратчайших путей между всеми узлами сети воз­ведением в r -ю степень структурной матрицы длин 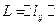, но при возведении в степень матрицы L предлагается использовать специальные операции, которые определяются сле­дующими действиями:

1) операция умножения двух величин х и у при возведении мат­рицы в степень соответствует, в описываемом методе, их алгебраи­ческой сумме, т. е. 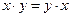соответствует ;

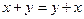2) произведение бесконечности на любое число равно бесконеч­ности;

3) сумма двух величин равна минимальному из слагаемых, т. е. 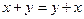соответствует .

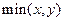Можно показать, что при использовании предлагаемых опера­ций возведение в r -ю степень матрицы L является не чем иным, как одним из способов получения величины - кратчайшего пути из i в N, имеющего 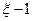промежуточный узел.

Действительно, возведение матрицы L в r-ю степень можно рассматривать как последовательное (г — 1) - кратное умножение матрицы L саму на себя:

.

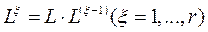Если 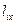является элементом i строки х столбца матрицы L, а - элементом х строки j столбца матрицы , то по обычным правилам умножения матриц элемент i строки и j столбца , матрицы 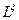будет равен:

.

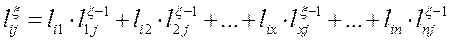С учетом операций, введенных Шимбелом, выражение запишется следую­щим образом:

,

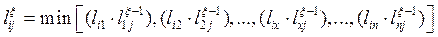или в сокращенном виде

. (5.4)

Нетрудно убедиться в том, что 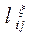в выражении (5.4) при j = N равно . В самом деле,

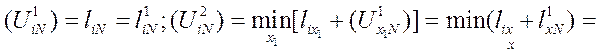
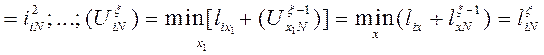
Поэтому , при 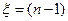, является величиной кратчайшего расстояния от узла i к узлу j.

Таким образом, вычислив последовательно элементы матрицы 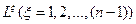, используя метод Шимбела, мы получаем матрицу кратчайших расстояний между узлами сети.

Следует отметить, что при возведении матрицы L в степень существует предел, при котором

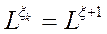(5.5)

т. е. дальнейшее умножение матрицы не приводит к измене­нию элементов матрицы

Величина 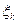, при которой выполняется равенство (5.5), оп­ределяется максимальным числом ветвей в кратчайшем пути между какой-либо парой узлов сети и, следовательно,

.

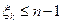Поэтому, как только в процессе возведения в степень матрицы L на­чинает выполняться равенство (5.5) дальнейшие вычисления можно прекратить, а полученная матрица 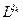будет матрицей крат­чайших путей.

Матрицу кратчайших путей 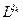иногда называют дисперсион­ной матрицей D, т. е.

.

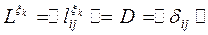Метод, предложенный Оттерманом, является дальнейшим развитием метода Шимбела. Он позволяет получить не только величину первых, вторых, третьих и т. д. кратчайших путей, но и сами пути (перечень узлов, через которые эти пути проходят).

Как и в описанном ранее методе Шимбела, получение кратчай­ших путей в методе Оттермана производится путем преобразований структурной матрицы длин .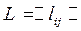

Вначале, пользуясь методом Шимбела, определяется дисперсионнаяматрица 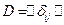(матрица кратчайших путей )

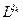Затем из структурной матрицы длин L образуется модернизированная матрица длин 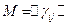, которая получается заменой в структурной матрице длин L значений элементов главной диагонали с 0 на .

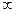Полученная указанным способом модернизированная матрица длин М умножается на дисперсионную матрицу D c использованием операций, введенных Шимбелом.

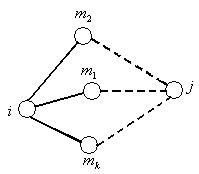
Рис. 5.2

При умножении матрицы М на матрицу D образуется матрица 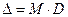, элементы которой используются для получения дистан ­ ционных матриц (матриц величин 1-го, 2-го и т. д. кратчайших путей) и матриц маршрутов, содержащих номера узлов на выбранных кратчайших путях.

Каждый элемент 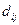матрицы 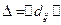, получаемой при умно­жении матриц М и D с учетом операций, введенных Шимбелом, бу­дет иметь вид:

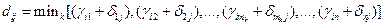
или в сокращенном виде:

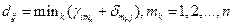. . (5.6)

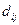Каждое из выражений вида , входящее в элемент , определяет длину пути от узла i к узлу j, если первым проме­жуточным узлом после узла i на этом пути будет узел 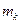(рис. 5.2).

Величина самого минимального из всех выражений, входящих в элемент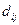, определяющая длину самого короткого пути от узла i к узлу j:

,

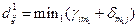заносится в качестве элемента (i, j) в дистанционную матрицу 1-го вы­бора, а значение т₁ этого выражения заносится в качестве элемента (i, j) в матрицу маршрутов 1-го выбора. Второе по величине выражение из элемента 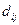, являющееся длиной второго кратчайшего пу­ти между узлами i и j:

,

заносится в качестве элемента (i, j) в дистанционную матрицу 2-го выбора, а т₂ - в матрицу маршрутов 2-го выбора.

Выражение

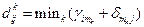(5.7)

заносится в дистанционную матрицу k- го выбора, а 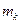- в матрицу маршрутов k- го выбора.

Как видно из выражения (5.7), элементы матрицы , полу­ченной умножением матрицы М на матрицу D, содержат перечень всех путей между парами узлов сети, из которых и производится выбор 1-го, 2-го и т. д. кратчайших путей. Использование для этой цели матрицы М вместо матрицы L вызвано необходимостью исключить из рассмотрения выражения вида 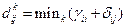, которые приводят к записи в матрицу маршрутов k -го выбора в качестве элемента (i, j) узла i. Это будет означать, что движение по пути от узла i к узлу j должно прохо­дить через узел i, что не дает для управления никакой дополнитель­ной информации.

Приведенный выше метод определения кратчайших путей 1-го, 2-го,…, k-го и т. д. выбора не исключает возможности появления петель в выбранных путях, т. е. случаи, когда какой-либо путь проходит через один и тот же узел два или более раз.

В рассматриваемом Оттерманом методе вводятся два условия, проверка и выполнение которых исключает возможность появлений петель.

Условие 1. Выявление и исключение петель в кратчайших путях 1-го выбора.

Рассмотрим кратчайший путь 1-го выбора между произвольной парой узлов y и z сети (рис.5.3). Выберем на этом пути произволь­но три узла - узел i, узел j и узел x, который находится между узлами i и j на рассматриваемом кратчайшем пути.

Здесь возможно появление петли в том случае, если кратчайший путь 1-го выбора от узла х к узлу j проходит через узел i. В этом случае путь 1-го выбора от узла y к узлу z будет проходить через узел i к узлу x и далее, кратчайшим путем от x через i к j, образуя петлю.

Из сказанного следует условие, гарантирующее отсутствие петель в кратчайших путях 1-го выбора.

Кратчайший путь 1-го выбора между произвольной парой узлов y и z сети не будет содержать петель, если для трех произвольно взятых узлов, лежащих на этом пути, узла i, узла j и промежуточного (между i и j) узла x выполняется неравенство:

(5.8)

где 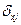, , 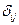- кратчайшие расстояния между парами узлов (i, j) (x, i) (i, j) соответственно (элементы дисперсионной матри­цы D).

Рис. 5.3

Проверка условия 1 при составлении дистанционных матриц и матриц маршрутов 1-го выбора и исключение из этих матриц путей, не удовлетворяющих условию 1, позволяет получить систему крат­чайших путей 1-го выбора, не содержащих петель.

Условие 2. Выявление и исключение петель в путях 2-го, 3-го и т. д. выбора.

Выполнение условия 1 исключает возможность появления пе­тель в путях 1-го выбора, но не гарантирует отсутствия петель в путях 2-го, 3-го и т. д. выбора.

Чтобы избежать появления петель в пути 2-го, 3-го и т. д. выбо­ра, вводится условие 2, смысл которого заключается в том, что, двигаясь по пути от узла к узлу, мы должны всегда приближаться к конечному узлу z, т. е.

,

при условии, что узел 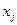при движении по пути от узла y к узлу z предшествует узлу .

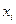Если условие 1 проверялось при составлении дистанционных матриц и матриц маршрутов, то условие 2 проверяется в процессе передачи сообщений по сети.

Условия 1 и 2 полностью исключают возможность появления петель, однако выполнение этих условий приводит к запрещению большого числа путей, что, естественно, ограничивает возможности сети по передаче сообщений.

Пример. Действие описанных выше матричных методов определения кратчайших путей рассмотрим на примере уже использованной ранее сети, имеющей структурную матрицу длин:

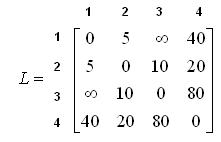
В первую очередь, как в методе Шимбела, так и в методе Оттермана необходимо путем возведения матрицы 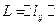в r- ю степень, 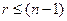, получить дисперсионную матрицу .

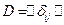Используя выражение (5.4), получим сначала матрицу , а

затем и .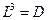

Элемент матрицы , согласно (5.4) определится как

.

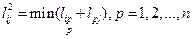Отсюда

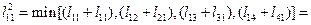
(Выражения 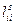можно не определять, так как из матрицы L и выражения (5.4) видно, что ).

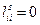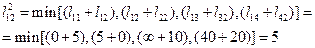
Определяя аналогичным образом остальные элементы 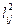, получим матрицу

Подобным же образом можно получить и матрицу 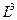, элементы которой

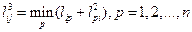
Например,

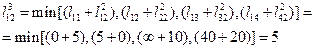
После определения всех 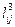матрица 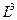будет иметь вид

Матрицы и 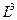оказались равны друг другу. Это получилось потому, что в рассматриваемой сети не нашлось ни одного кратчай­шего пути, имеющего более одного транзитного узла.

Полученная дисперсионная матрица содержит величины кратчайших расстояний между всеми парами узлов сети.

Помимо получения дисперсионной матрицы, в методе Оттермана предусматривается еще и получение дистанционных матриц и мат­риц маршрутов кратчайших путей 1-го, 2-го и т. д. выбора. Для этой цели берется модернизированная матрица длин 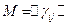, получаемая из исходной матрицы L заменой элементов главной диа­гонали на :

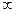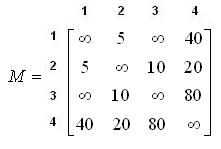
и умножается с применением операций Шимбела на дисперсионную матрицу D:

.

Элементы 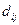матрицы можно определить, пользуясь выра­жением (5.7).

Так, из выражения (5.7) для рассматриваемой сети

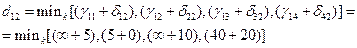
Самая минимальная из сумм, составляющих 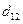, а именно, 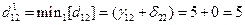, заносится в качестве эле­мента 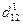дистанционной матрицы маршрутов 1-го выбора, а зна­чение индекса p в этой сумме, р = 2, - в качестве элемента 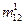маршрутной матрицы 1-го выбора.

Вторая по величине сумма 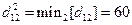и значение p для этой суммы, p = 4, заносится в дистанционную матрицу и мат­рицу маршрутов 2-го выбора, третья по величине сумма заносится в матрицы 3-го выбора и т. д.

Определив указанным выше, образом все элементы матрицы 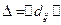и распределив их значения и индексы по дистанционным матрицам и матрицам маршрутов, получим совокупность дистан­ционных матриц, определяющих длину пути 1-го, 2-го и З-го выбо­ра, и совокупность матриц маршрутов, определяющих промежу­точные узлы этих путей:

Д и с т а н ц и о н н ы е м а т р и ц ы

М а т р и ц ы м а р ш р у т о в

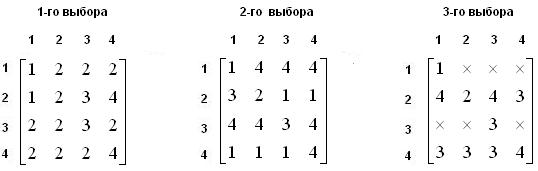
Числа в этих матрицах маршрутов указывают, через какие узлы реализуются пути 1-го, 2-го, 3-го выбора для любой пары узлов. Эти данные могут быть использованы для построения матриц маршрутов о которых шла речь в предыдущих параграфах.

Как и следовало ожидать, дистанционная матрица 1-го выбора полностью совпала с дисперсионной матрицей D.

Для выявления и исключения петель в путях 1-го выбора необходимо проверить для всех кратчайших путей выполнение нера­венства (5.8). Для этого определяем перечень всех путей между узлами сети.

В рассматриваемом примере проверим наличие петель в крат­чайших путях, связывающих, например, узел y = 1 и узел z = 2, 3, 4.

Для y = 1 и z = 2 из матрицы маршрутов 1-го выбора определя­ем, что кратчайший путь от узла 1 к узлу 2 не имеет промежуточных узлов и поэтому не может иметь петель (неравенство (5.8) про­верять не имеет смысла).

Для у = 1 и z = 3 кратчайший путь от узла 1 к узлу 3, согласно матрице маршрутов 1-го выбора, проходит через узел 2. Для этого случая неравенство (5.8) будет иметь вид 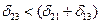; под­ставив в неравенство соответствующие значения 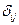из дисперсион­ной матрицы D, получим

10 < (5 + 5). Неравенство удовлетво­ряется, и кратчайший путь между узлами 1 и 3 не содержит петель.

Для y = 1 и z = 4 неравенство (5.8) 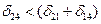также удовлетворяется.

Аналогичным образом проверяются кратчайшие пути между всеми парами узлов, и все пути, содержащие петли, исключаются.

Как уже указывалось, проверка и исключение петель из путей 2-го, 3-го и т. д. выбора производится на узлах по матрице маршру­тов и дисперсионной матрице, хранящейся на этом узле.

Пусть в рассматриваемом нами примере необходимо передать сообщение от узла 1 к узлу З.

Как видно из матрицы маршрутов 1-го выбора, первый кратчай­ший путь от узла 1 к узлу 3 проходит через узел 2.

Второй кратчайший путь должен проходить, согласно матрице маршрутов 2-го выбора, через узел 4. Чтобы убедиться, что второй кратчайший путь не содержит петель, проверяем неравенство (5.9), которое для нашего случая будет иметь вид 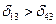. Из дисперсионной матрицы видно, что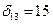, а 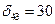. Неравенст­во не удовлетворяется, и второй кратчайший путь может содержать петлю. Действительно от узла 4 к узлу 3 кратчайший путь лежит через узел 2, а если ветвь сети между узлами 2 и 3 занята, то сообще­ние по второму кратчайшему пути от узла 2 к узлу 3 пройдет через исходный узел 1, образуя петлю. Следовательно, использование второго кратчайшего пути от узла 1 к узлу 3 может привести к обра­зованию петли, если первые кратчайшие пути окажутся занятыми или поврежденными.

Подобным же образом проверяются пути между остальными парами узлов.

Контрольные вопросы:

1) Назовите и поясните назначение путевых процедур и классификацию методов маршрутизации?

2) Назовите требования, предъявляемые к алгоритмам маршрутизации, и поясните их?

3) В чем разница между адаптивными и неадаптивными методами маршрутизации. Назовите и поясните, какие методы маршрутизации относятся к неадаптивным?

4) Расскажите в чем заключается метод определения кратчайших путей с помощью нумерации узлов и ветвей?

5) Объясните суть матричных методов определения кратчайших путей. Дайте определение дисперсионной и дистанционной матриц. Назовите два условия исключающих возможность появлении петель?

Задача:

Задана сеть, содержащая п = 4 узла. Определить кратчайший путь от всех узлов сети к узлу № 4 по методу нумерации узлов и ветвей

(граф, отображающий рассматриваемую сеть, представлен на рисунке; цифры, стоящие у каждого ребра графа, обозначают его длину).

Дата добавления: 2014-01-07