Критерии индивидуального выбора

Различные критерии оптимального выбора являются следствиями аксиомы рационального поведения, которая гласит: ЛПР выбирает решение так, чтобы максимизировать значение функции предпочтения. Это утверждение формально можно записать в виде

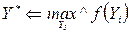(54)

где Y^* – оптимальное решение. Практика показывает, что аксиома рационального поведения выполняется в подавляющем большинстве случаев.

Выбор того или иного конкретного критерия связан с определением стратегии выбора ЛПР. Он должен четко сформулировать, будет ли он действовать осторожно, рассчитывая на наихудший случай, или будет действовать с большим риском, рассчитывая на оптимистический, наилучший случай, или, наконец, его стратегия при выборе будет основана в расчета на некоторые средние условия. Перечисленные три стратегии определяют три группы критериев выбора. Поэтому формулировка критерия основана на определении стратегии выбора. Критерий является конкретным инструментом для проведения расчетов в целях получения оптимального решения.

Рассмотрим из ряда конкретных критериев индивидуального выбора решение «критерий максимума среднего выигрыша К».

Пусть имеется множество ситуаций s = (s₁,..., s_n) с вероятностями появления Р = (Р₁, Р₂,..., Р_n) и множество допустимых решений Y_Д = (Y₁, Y₂,..., Y_m). На множестве ситуаций и решений определена функция предпочтения, оценивающая степень достижения каждым решением одной или всей совокупности целей

.

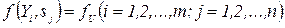Поставим в соответствие каждому решению коэффициенты а_i (i = 1, 2,..., m). Эти коэффициенты определяются предпочтениями решений и вероятностями ситуаций. Алгоритмы их вычисления будут рассмотрены далее отдельно для случаев количественных и качественных измерений. Чем больше коэффициент, тем более предпочтительным является соответствующее ему решение.

Используя коэффициенты решений, критерий максимума среднего выигрыша представим в виде

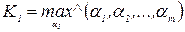
Эта запись означает, что необходимо выбрать из множества коэффициентов наибольший. Номер наибольшего коэффициента определяет номер решения, которое является оптимальным.

Если предпочтения измеряются в количественных шкалах, то коэффициенты решений в случае среднего выигрыша вычисляются как сумма взвешенных вероятностями ситуаций значений функции предпочтения.

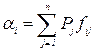(55)

Рассмотрим частные случаи. Пусть достоверность появления всех ситуаций одинакова, т.е. все вероятности равны между собой. Поскольку сумма вероятностей ситуаций равна единице, то при равенства вероятностей получаем, что все они равны Р_j = 1 / n, где n – количество ситуаций. В этом частном случае коэффициенты решений вычисляются по формуле

(56)

Множитель 1 / n не влияет на определение максимума, поэтому коэффициенты можно вычислять по формуле

(57)

Если имеет место только одна ситуация, например s_k, то ее появление является достоверным и, следовательно, Р_k = 1. Остальные ситуации имеют нулевые вероятности появленкя: Р_j = 0, j ¹ k. В этом случае коэффициенты решений непосредственно равны значениям функции для k -той ситуации

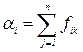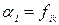т.е. (58)

Рассмотрим теперь измерение функция предпочтения в порядковой шкале, осуществляемое методами ранжирования или парного сравнения. Коэффициенты решений вычисляются по следующим формулам:

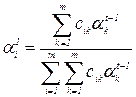, (i = 1, 2,..., m; t = 1, 2) (59)

Здесь t – номер шага приближения, с_ik – элементы осредненной по ситуациям матрицы парных сравнений решений, вычисляемые по формулам:

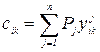(60)

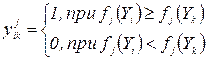(61)

В выражении (60) Р_j – вероятности ситуаций, n – количество ситуаций, y_ik^j – i, k-й элемент матрицы парных сравнений решений для j -й ситуации, f_j(Y_i) – функция предпочтения Y_i -го решения j -й ситуации.

Пример 4. Определить оптимальное по критерию среднего выигрыша решение Y^* из множества трех допустимых решений Y₁, Y₂, Y₃ для случая четырех ситуаций s₁, s₂, s₃, s₄, ЛПР определил предпочтения решения для каждой ситуации в количественной шкале, которые приведены в табл. 21. В нижней строке этой таблицы даны вероятности ситуаций.

По формуле (55) вычислим коэффициенты решений a_i. Результаты вычислений представлены в последней колонке табл. 21. Очевидно, что максимальным является коэффициент a_i = 5,2, поэтому оптимальным является решение Y^* = Y₁.

Пример 5. Определить оптимальное по критерию среднего выигрыша решена из множества трех допустимых решений Y₁, Y₂, Y₃ для случая трех ситуаций s₁, s₂, s₃ вероятности появления которых Р₁, Р₂, Р₃ известны. ЛПР определил предпочтения решений для каждой ситуации в порядковой шкале. В табл. 22 представлены значения функции, предпочтения в рангах и вероятности ситуаций.

Таблица 21

sj Yi	s1	s2	s3	s4	ai
Y1					5,2
Y2					4,5
Y3					5,0
Pi	0,1	0,2	0,5	0,2

Таблица 22

sj Yi	s1	s2	s3
Y1
Y2
Y3
Pi	0,5	0,3	0,2

Для каждой ситуации s_j запишем предпочтения решений в виде матрицы парных сравнений, руководствуясь правилом (21) и ранжировками табл. 22. В табл. 23-25 представлены матрицы парных сравнений || J_ik¹ ||, || J_ik² ||, || J_ik³ || соответственно для ситуаций s₁, s₂, s₃.

Для построения обобщенной матрицы парных сравнений в соответствии с формулой (60) просуммируем произведения матриц 23-25 на вероятности ситуаций (нижняя строка в табл. 22). Результаты вычислений представлены в табл. 26.

Вычислим коэффициенты решений первого приближения, воспользовавшись формулой (59) при t = 1. Возможность ограничиться только первым приближением обусловлена тем, что достаточно знать коэффициенты решений с точностью до порядка, поскольку последующая операция определения максимума требует знания только порядковых чисел, а не точ­ных значений коэффициентов. Выполняя вычисления, получим вектор коэффициентов решений

a₁ = 0,45; a₂ = 0,35; a₃ = 0,2.

Наибольшим является коэффициент первого решения a₁ = 0,45, поэтому операция максимума приводит к выбору коэффициента a₁. Поскольку это коэффициент первого решения, то оптимальным по критерию максимума среднего выигрыша является решение Y₁.

Таблица 23

	Y1	Y2	Y3
Y1
Y2
Y3

Таблица 24

	Y1	Y2	Y3
Y1
Y2
Y3

Таблица 25

	Y1	Y2	Y3
Y1
Y2
Y3

Таблица 26

c11 = 1	c12 = 0,7	c13 = 1
c21 = 0,3	c22 = 1	c23 = 0,8
c31 = 0	c32 = 0,2	c33 = 1

Дата добавления: 2014-01-07