Различные задачи аппроксимации

Термин «аппроксимация» происходит от латинского approximum – ближайший, и означает приближение чего-нибудь, т.е. замена данного объекта некоторым другим, близким к нему. В данной теме речь пойдет о приближении функций.

Условия задачи: некоторая функция у = у (х) задана таблицей:

х 0	х 1	….	хn
y 0	y 1	….	yn

в (n + 1) точках (узлах). Необходимо определить, хотя бы приблизительно, значение у (х) при х ¹ х_i. То есть надо построить Y (x) – аппроксимирующую функцию, такую, что у (х)» Y (x) для всех х Î [ х ₀, х_n ].

В такой постановке задача имеет бесчисленное количество решений. Чтобы решение было единственным, необходимы дополнительные условия:

1°. Надо указать класс функций, в котором будем искать Y (x) (многочлены, тригонометрические, дробно-рациональные или иные функции).

Обычно в качестве Y (x) используются функции либо легко вычисляемые, либо подходящие по физическому смыслу задачи. Например, если у (х) описывает некоторый периодический процесс (звуковые колебания или иные схожие явления), то естественно искать Y (х) среди тригонометрических функций. Часто в качестве Y (х) используется многочлен.

2°. Надо указать критерий близости у (х) и Y (x).

Наиболее часто применяются следующие критерии.

1) у (х_i) = Y (x_i) – требуется точное совпадение в заданных узлах исходной и аппроксимирующей функции. Задача аппроксимации при таком дополнительном условии называется задачей интерполяции.

2) Близость обеспечивается условием

,

т.е. в отличие от задачи интерполяции, точного совпадения в узловых точках не требуется. Такая задача называется задачей среднеквадратичного приближения.

3) Близость обеспечивается условием

.

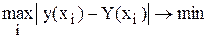Т.е. среди всех отклонений D _i = | у (х_i) – Y (x_i) | выбирается самое большое и стремятся минимизировать его. Такая задача называется задачей равномерного или Чебышевского приближения.

Вследствие различной постановки задачи аппроксимации получаем разные решения.

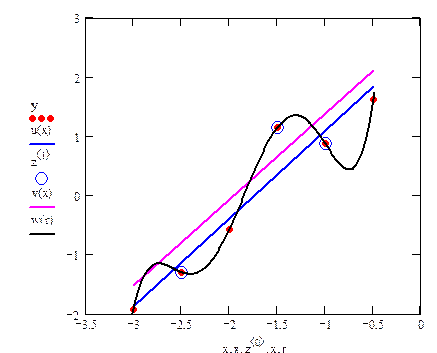
Пример 3.1. На рис. 3.1 приведены примеры различной аппроксимации функции, заданной в таблице 3.1

Таблица 3.1
xi	-3	-2.5	-2	-1.5	-1	-0.5
yi	-1.92	-1.3	-0.57	1.15	0.88	1.63

Во всех случаях в качестве Y (x) выбирается многочлен.

В задаче интерполяции кривая Y (x) проходит через все точки, для этого надо взять многочлен достаточно высокой степени, в данном случае – пятой.

Поскольку все точки табличной функции лежат практически на одной прямой, кроме 4-й точки, то в задаче среднеквадратичного приближения выбран многочлен первой степени. Полученная прямая (нижняя на графике) проходит вблизи от всех точек, кроме 4-й. Тем самым среднее отклонение получается минимальным.

При равномерной аппроксимации максимальное отклонение между табличными точками и аппроксимирующей непрерывной линией (верхняя прямая) достигается в трех выделенных узлах. На графике видно, что эти отклонения совпадают по модулю, но различаются по знаку. Благодаря этому максимальное отклонение будет минимально. Если аппроксимирующая линия пройдет выше или ниже, чем на графике, то какие-то отклонения увеличатся, и минимума не будет.

Рис. 3.1. Решения различных задач приближения функции, заданной таблично

Если Y (x) = P_n (x) – многочлен n -й степени (напоминаем, что n + 1 – число точек) и Y (x_i) = у (х_i), то при таких условиях мы имеем задачу классического (многочленного) интерполирования. Эта задача применяется, когда выполнены следующие условия.

1) n £ 5.

2) Значения у_i не содержат ошибок.

3) Функция у (х) гладкая.

4) х_i изменяются в достаточно узком диапазоне, т.е. требуется локальное приближение.

В принципе эту задачу можно решить, сведя её к решению системы линейных уравнений. Многочлен n -й степени имеет вид:

P _n (x) = a ₀ + a ₁ x + a ₂ x ² + … + a_n xⁿ.

Задача интерполяции состоит в том, чтобы найти коэффициенты многочлена. По условию должно быть у_i = Y (x_i) = P _n (x_i). Следовательно, имеем систему из n + 1 уравнений относительно n + 1 неизвестных коэффициентов:

. i = 0, 1,…, n (3.1)

Доказано, что если все x_i различны, то решение системы единственно. Однако

1) при больших n система (3.1) плохо обусловлена;

2) для многих задач желательно иметь явное решение, т.е. формулу для вычисления коэффициентов.

Поэтому рассмотрим другой метод решения задачи многочленного интерполирования.

Дата добавления: 2014-01-07