Алгоритмическое определение булевских операций

Булевский тип.

(Boolean, в честь Джорджа Буля, основоположника мат. логики)

Множество значений: {true, false}

Множество операций: все сравнения над некоторыми типами имеют булевское значение.

В паскале не допустимы кратные сравнения: 1<sqr(x)+sqr(y)<n

Функции алгебры логики

not b ┐b отрицание

b1 and b2 b1&b2 конъюнкция

b1 or b2 b1vb2 дизъюнкция

Boolean x Boolean → Boolean

b	not b		b1	b2	b1 and b2		b1	b2	b1 or b2
true false	False True		true false false true	true true false false	true false false false		True true false false	true false true false	true true true false

Отрицание

Конъюнкция

a) b)

Эти 2 определения блок-схем не эквивалентны, если рассматривать неопределенное значение переменных.

b₁=false b₂=0.

Вторая блок-схема соответствует классическому определению конъюнкции: если хотя бы один из элементов функции не определен, то и функция не определена.

Вариант «а» дает так называемое быстрое означивание конъюнкции. Строго говоря, это другая, отличная от конъюнкции операция, которая часто обозначается “cand” или условный (conditional and, но не в паскале). В паскале обозначение and используется для обеих операций. Точная семантика реализуется директивой компилятора. {$B±}

Пример: найти номер заданного значения в последовательности из n чисел

Вариант 1

i:=1; while (i≤n) and (a[i]=x) do i:=i+1;

1. i:=1; read(a); while (i≤n) and (a=x) do begin

read(a);

i:=i+1;

end;

2. i≤n) and (a[i]=x)

Рекомендации: не полагаться на разную семантику булевских операций, не допускать неопределенности выражений. Те же соображения приложимы к определению дизъюнкции, true or 0.

Замечания по программированию условий:

Упрощение отрицания not(not­­_b)=b

not(b₁ and b₂)=not b₁ or not b₂

not(b₁ or b₂)=not b₁ and not b₂

Удобство применения булевских выражений: можно избегать многочисленных вложений условных операторов, делая алгоритмы еще более линейными.

Пример: линейный поиск.

Program poisk4(input,output);

Var a,x:integer;

found:boolean;

begin

found:=false;

read(x);

while not eof() and not found do

begin

read(a);

if x=a then found:=true;

end;

end.

Стратегия вычисления условий

Написание достаточно сложных условий само по себе требует некоторой системы.

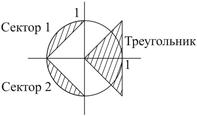Стратегия: разбить область на выпуклые фигуры, принадлежность точки к каждой из таких фигур определяется уравнением каждой из границ.

b:= (принадлежит сектору 1) or (принадлежит сектору 2) or (принадлежит треуг)

Принадлежит сектору 1:= (y>=x+1) and (sqr(x)+sqr(y)<=1)

Принадлежит сектору 2:= (y>-x-1) and (sqr(x)+sqr(y)<=1).

Принадлежит треугольнику:= (abs(y)<=x) and (x<=1).

Замечание: эта стратегия иллюстрирует важный факт в математической логике. Любое свойство можно записать в виде дизъюнкции элементарных конъюнкций.

Вычисление кванторов

Полный язык математической логики содержит кроме перечисленных выше булевских операций кванторные операции.

Зафиксируем некоторое перечисление элементов множества X:

X={x₁, x₂, x₃, …}

"x ÎX B(x)=B(x₁) and B(x₂) and B(x₃) …

$x ÎX B(x)=B(x₁) or B(x₂) or B(x₃) …

Рекуррентное определение кванторов

{b="xÎX B(x)}

b₀:=true

b_i+1:=b_i and b(x_i+1)

b:=true

i:=1

while (i<=n) and b do begin

if not B(x_i+1) then b:=false;

i:=i+1;

end;

Выяснить, является ли данная последовательность упорядоченной

Begin

assign(f,’input.txt’);

reset(f);

b:=true;

if eof(f)=false then

begin

read(f,ao);

while(eof(f)=false) and b do

begin

read(f,a);

if ao<=a then ao:=a

else b:=false;

end;

end;

writeln(b);

close(f);

End.

Пример вычисления квантора существования – задача поиска.

b:= $ iÎ[1..n] (x=a_i

Символьный тип

Множество значений: некоторое множество алфавитных символов, фиксированных данной версией языка. Любой такой алфавит считается упорядоченным, т.е. символьный тип – порядковый, значит определено c₁<с₂, если c₁ идет в алфавите раньше, чем с₂. Также succ(c), pred(c).

Известно, что любой алфавит содержит малые и большие латинские символы и буквы, причем они упорядочены в естественном смысле:

‘a’<’b’<’c’<…

‘A’<’B’<’C’<…

Переменная Буквенная константа

a ‘a’

‘0’<’1’<’2’<…

Кроме того, на символьном типе определены операции chr и ord.

chr(i) – выдает символ с заданным номером i

ord(a) – выдает номер символа

Символьный тип является универсальным в том смысле, что значение любого другого типа как-то обозначается в некоторой фиксированной системе обозначения.

Задача: определить данное целое число по его записи в десятичной системе.

Упражнение:

1. Определить данное целое число по его записи

2. Обратное: выяснить запись числа по его значению

Достаточно:

1. Научиться находить значения цифр (‘0’,’1’,…,’9’). Это решит задачу в случае символьной последовательности длиной 1.

2. Научиться вычислять значение числа по значению входящих в его запись символов.

‘2’,’0’,’0’,’1’

2•10³+0•10²+0•10¹+1•10⁰

Надо вычислить 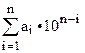со старшей цифры.

m=1 ord(c)-ord(‘0’)

m=2 n=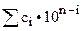

n+1=n_i•10+c_i

Обратная задача.

Дано число, перевести его в символьное представление.

1. nÎ[0,9] chr(n+ord(‘0’))

2. n=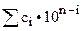

c_i+1=n_i mod 10

n_i+1=n_i div 10

Идея: вычислять c и n по рекуррентной схеме до тех пор, пока n не станет равно 0.

Недостаток решения: знаки порождаются в обратном порядке.

Упражнение 3: Найти схему порождения записи числа в «естественном» порядке.

Производные(структурные) типы

Массивы

A:array[I] of T, где Т произвольный тип (в стандарте, кроме файлов). I – произвольный конечный порядковый тип.

Семантика:

Множество значений:

1. частный случай: тип индексов I есть ограничение целого типа [1..n], [0..n]. В этом случае множество значений – класс всех последовательностей фиксированной длины n. Тип «массив» - статический; f: N®T, т.е. фу нкций из интервала [1,n]T

2. В общем случае значениями являются функции. f: I®T. I – не интервал, из I в T все функции на конечном множестве аргументов. Массив – явно определяемая, табличная функция (соответствие).

Операции над массивами

Единственная операция над массивами – операция выборки, синтаксис A[e] – A – имя массива, e – любое выражение типа I (a[e]=app(a,e) от двух переменных). Семантика зависит от места, занимаемой операции в присваиваниях.

Напомню, с точки зрения семантики мы рассматриваем (кратные) присваивания как стандартное обозначение любого оператора.

Справа в присваивании операция выборки означает вычисление массива (как функции) в заданной «точке», т.е. по аргументу-индексу.

Пример. y:=a[x]. Значение y становиться равным значению a(x).

При отдельном рассмотрении соответствующий оператор применения функции к аргументу называется оператором аппликации.

Слева в присваивании операция выборки означает переопределение массива (как функции) в заданном аргументе.

Пример. a[x]:=y. Значение a[x] становиться равным текущему значению переменной y.

В любом случае, значение индекса должно принадлежать области определения массива. В противном случае говорят об ошибке «выхода за границы массива».

Расширенный синтаксис. Массивы размерности n.

Пусть Т – произвольный тип (кроме файлового).

Для записи типа array[I₁] of array [I₂] of T и соответствующей перации выборки a [x][y] допустим более компактный синтаксис array[I₁,I₂] of T и a[i,j]

Аналогично вводятся обозначения вида array[I₁,…,I_n] of T и a[i₁,…,i_n];

Обычно такой случай связывается с матрицами размерности n.

Задача: подсчитать частоту вхождений каждой малой буквы в заданный текст.

Вычисляется функция: область определения – символы [‘a’, …, ‘s’], область значения – N (натуральные числа).

{k_i – количество вхождений i-ой буквы алфавита}

assign(f,’…’);

reset(f);

for c:=’a’ to ‘z’ do k[c]:=0;

while not eof(f) do

begin

read(f,c);

k[c]:=k[c]+1;

end;

close(f);

Статические массивы выглядят не очень естественным представлением данных в случае последовательностей произвольной длины или функций с расширяемой областью определения. В таких случаях более естественно рассматривать последовательности не более, чем заданной длины (функции, области определения которых содержаться в фиксированном множестве). Назовем такие массивы «псевдодинамическими».

Строки. Динамические массивы.

array of T.

Множество значений: все функции с множеством значений Т и областью определения nÎN.

Основная операция – операция выборки.

Описание переменной вида a: array of T в реальности определяет функцию с пустой областью определения. Потому, например, присваивание вида a[1]:=1; будет ошибкой.

Реальная область значений определяется динамически, т.е. в ходе выполнения программы с помощью оператора setlength(a,b); a – имя динамического массива; b – выражение, принимающее значения, натурального типа. Текущую длину можно определить с помощью функции length(а). Контроль за выходом за границы массивов в этом случае не осуществляется автоматически.

Обычная операция выборки имеет ту же семантику, что и для статических массивов. Другие (например присваивание) – нет. Смотри далее – ссылочный тип.

Упражнение: запрограммировать операции над последовательностями, представляя их псевдодинамическими и динамическими массивами.

1. Включение и удаление компоненты с заданным номером или заданным значением.

2. Объединение, разность, пересечение, множества компонент.

Динамические массивы появляются только в Object Pascal или Delphi, но задолго до этого появляется их частный случай – динамические символьные массивы или строки.

String имеет максимальную длину 255 символов. Кроме очевидных операций выборки, установки длины и функции длины, на типе определены следующие операции:

1. Конкатенация (сцепление)

S:=S₁+S₂, где S₁=c₁,…,c_n, S₂= c₁^¢…c_m¢, S=c₁,…,c_n,c₁^¢…c_m¢

2. Предикат сравнения строк. Словарный (лексикографический) порядок: S₁<S₂, S₁=c₁…c_n, S₂=c₁^¢…c_m¢. Пусть i – наименьшее число, такое что c_i<c_i¢. Если такого i не найдено, то строки равны. S₁<S₂, если c_i<c_i¢ в смысле установленного ранее порядка на типе char.

‘шабаш’<‘шалаш’

‘шабаш’<‘шабашка’

В случае неодинаковой длины считаем что меньшее слово дополнено нужным количеством пустых символов, которые меньше любого символа алфавита.

В Паскале тип string не считается порядковым, но соответственные функции succ и pred не трудно определить.

Упражнение: сделай это J

Комбинированные типы и записи

Record

N₁: T₁;

……..

N_m: T_m;

End.

Значениями типа «запись» являются функцией с областью определения, состоящей из имен N₁,…,N_m. Причем f(N₁)ÎT_i "i=1,…,m

В математике такая конструкция называется именованном декартовым произведением.

Просто декартовым произведением называется множество всех последовательностей длины m, таких, что t_iÎT_i.

Например

Real²=Real•Real

{<t₁,t₂>, t₁Îreal, t₂Îreal}

Запись – это набор переменных N₁,…,N_m, типа T₁,…,T_m, воспринимаемый как единое целое. Основная операция – операция выборки, с той же семантикой, что и у массивов, но с другим синтаксисом.

r.N_i, где r – переменная тип «запись», N_i – одно из имен N₁,…,N_m.

Понятие «запись» не вычислительное, а логическое – это описание состояния некоторого объекта.

type

tTochka = record

x,y: real;

end;

{x,y – декартовы координаты точки}

record

ugol,radius: real;

end;

{полярные координаты точки}

Вычислить значение многочлена

Begin

read(n,x,a);

s:=a; k:=1;

for i:=1 to n do

begin

read(a);

k:=x•k;

s:=s+a•k;

end;

write(s);

End.

Уточним постановку: вычислить многочлен над комплексными числами.

Type complex=record

re:real;

comp:real;

end;

Var i,n: integer;

l:real;

x,a,k,s: complex;

Begin

read(n,x.re,x.comp,a.re,a.comp);

s.re:=a.re;

s.comp:=a.comp;

k.re:=1;

k.comp:=0;

for i:=1 to n do

begin

read(a.re,a.comp);

l:=k.re;

k.re:=x.re•k.re-x.comp•k.comp;

k.comp:=x.re•k.comp+l•x.comp;

s.re:=s.re+a.re•k.re-a.comp•k.comp;

s.comp:=s.comp+a.re•k.comp+a.re•x.comp;

end;

if s.comp<0

then

write(s.re,‘-’,abs(s.comp))

else

write(s.re,‘+’,abs(s.comp));

End.

Упражнение: написать программу зачисление абитуриентов в университет. В ходе зачисления используется информация:

1. ФИО

2. уникальный код абитуриента

3. оценка за экзамен

4. зачет/незачет по русскому языку

5. наличие медали

Абитуриент зачисляется, если он либо имеет медаль и 5 за первый экзамен, либо не имеет двоек и его средний балл больше проходного (считаем, что проходной балл уже подсчитан).

Оператор присоединения

Для того чтобы избежать необходимости выписывать полное точечное обозначение поля записи можно применять оператор присоединения вида: with r do s, где r – имя переменной типа «запись», а s – один оператор, в котором вместо имен вида r.N_i можно использовать имена вида N_i.

Семантика: оператор эквивалентен выполнению оператора S, в котором все имена вида N_i заменены именами вида r.N_i.

Типизированные файлы.

file of T, где Т – произвольный статический тип, кроме файла.

Семантика: последовательность компонент типа Т, произвольной длины.

Операторы: Assign (AssignFile), reset, rewrite, eof, close (CloseFile) – имеют ту же семантику. Операторы read и write имеют очевидную семантику, но другой синтаксис.

Read(f,v), где f – имя файла, v – единственная переменная типа Т.

Write(f,e), где f – имя файла, где е – единственное выражение типа Т.

Понятие строки и операции readln, writeln, eoln в этом случае не определены.

Упорядоченные файлы

Паскаль не использует явно понятие упорядоченного типа, хотя в математическом или абстрактном смысле они представляют собой тип данных с явно выраженным набором операций.

Для любого i Î [1,len(a)] (a_i<=a_i+1)

Для любого i,j Î [1,len(a)] (i<=j → a_i<=a_j)

Упорядоченность используется в программировании для создания более эффективных алгоритмов решения задач, в первую очередь задач поиска.

Поиск в упорядоченном файле

Found:=

a_i=x

$ iÎ[1,len(a)] (a_i>=x)

Идея: достаточно найти первое i, такое что x<=a_i, тогда found:=true Û x=a_i, если таковое существует; если такового нет, то found:=false.

Итак, поиск такого первого i: a_i>=x

found1:=$i (a_i>=x)

assign(f,’…’);

reset(f);

found1:=false;

while (not found1) and (not eof(f)) do

begin

read(f,a);

if a>=x then found1:=true

end;

if found1 then found:=a=x

else found:=false;

Арифметика упорядоченных файлов

Упражнение: Найти разность, объединение, пересечение упорядоченных файлов. Результат - так же упорядоченный файл.

Мотивация: Упорядочить файл – тяжёлая задача, не имеющая эффективного решения (однопроходного алгоритма). Гораздо проще сохранять упорядоченность файлов. Все алгоритмы – однопроходные.

Разность файлов:

f₃=f₁\f₂

reset(f₁);

reset(f₂);

rewrite(f₃);

while

begin

read(f₁,x);

If {xÏf₂} then write(f₃,x);

end

Задача решена, если для проверки включения использовать предыдущий алгоритм и учесть, что файл f₁ также упорядочен, а значит поиск в файле f₂ первого элемента b_i>=a_i не портит такого поиска для следующего элемента a_i, то есть b_j¢>=b_j.

Дихотомический поиск в упорядоченном массиве

Program Binar;

Var a:array[1..n] of integer;

l,r,m:integer;

found:boolean;

Begin

{ввод a}

l:=1;

r:=n;

found:=false;

while (l<=r) and not found do

begin

m:=(l+r) div 2;

if a[m]=x

then found:=true

else if a[m]<x then l:=m+1

else r:=m-1;

end;

end.

{Текст программы взят из книги, а не с лекции, но большой разницы быть не должно, т.к. алгоритм один}

Простые алгоритмы сортировки

Сортировка простым обменом

"i (a_i<=a_i+1)

"i,j (i<=j → a_i<=a_i+1)

Сортировка вставкой определяется в терминах операции вставки

а:=вставка(а,х)

a₁<=…<=a_n x

Begin

{ввод a}

for k:=2 to n do

begin

x:=a[k];

j:=k-1;

while (j>0) and (x<a[j]) do

begin

a[j+1]:=a[j];

dec(j);

end;

a[j+1]:=x;

end;

End.

{Текст этой программы также взят из книги, абсолютно уверен в несоответствии этой программы и программы на лекции, но идея одна}

На шаге «0» упорядоченная часть состоит из 1 элемента, неупорядоченная – из всех остальных. На i-ом шаге алгоритма берём первый элемент a_i из неупорядоченной части и вставляем его в уже упорядоченную к этому шагу часть; Достаточно n-1 шага.

Найти наибольшее j, такое что a_j<a_i, если оно есть, если нет поставить a_i на место a_j+1, т.е. сдвинуть все элементы начиная с места j+1 на единицу вправо, а потом на освободившееся место поставить a_i.

Множества

Синтаксис: set of T, где Т – произвольный порядковый тип.

Семантика:

Значения типа set of T – произвольные конечные совокупности значений вида a₁, …,a_n типа Т. Рассматриваемые совокупности не считаются упорядоченными. Все множества, полученные перестановкой элементов a₁, …, a_n считаются равными.

Синтаксис констант [E₁, …, E_n], где E_i – есть выражение типа Т, либо интервалы вида Е_i¹ … E_j², где Е_i¹ … E_j² – выражение типа Т, например [2,2,1,…,7].

Операции над множествами

1. Предикаты.

X in S ~ XÎS

S₁<=S₂ ~ S₁ S₂

2. Теоретико-множественные операции.

S₁+S₂ ~ S₁ÈS₂

S₁*S₂ ~ S₁ÇS₂

S₁-S₂ ~ S₁\ S₂

3. Эквивалентность теоретико-множественных и логических обозначений.

Любое множество однозначно связывается с формулой – характеристической формулой (предикатом множества).

F_s(x)=true(~)xÎS

Сопоставим теоретико-множественные операции, логические операции над предикатами.

x Î S ~ F_s(x) =true

S₁ S₂ ~ " x Î S₁ (x Î S₂)

x Î S₁ È S₂ ~ f_s1(x) or f_s2(x)

x Î S₁ Ç S₂ ~ f_s1(x) and f_s2(x)

x Î S₁\ S₂ ~ f_s1(x) and not f_s2(x)

Двойственность теории множеств и логики можно использовать для компактной записи свойств.

((x>=1)and(x<=10)) or ((x>=20)and(x<=40))

x:n[1..10]+[20..40]

Дата добавления: 2014-01-07