Проблема багатозначності критеріїв оптимальності і її рішення

Математичні методи оптимізації дозволяють знаходити оптимальні рішення тільки для одного критерію оптимальності. Але часто приходиться шукати рішення задачі, у якій необхідно досягати відразу кілька мет. Досить згадати гасло: Дамо більше взуття кращої якості і по більш низькій ціні. Можна просто привести у відповідь прислів'я: За двома зайцями поженешся жодного не піймаєш. Але існують методи, що дозволяють вирішувати і такі задачі. Якщо об'єкт оптимізації необхідно оцінити декількома критеріями, то вибирають звичайно компромісний варіант. У деяких випадках можлива формалізація вибору компромісного варіанта на основі методів кваліметрії.

Нехай нам необхідно максимізувати сумарну цінність зроблених продуктів. Це класична задача. Але додамо до цьому максимальний випуск продукту першого типу.

(А)

(В)

Першим виходом є зведення многокритериальной задачі до однокритериальной. Для цього привласнюють ваги кожному з критеріїв з поза модельними розуміннями (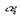, , 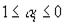). Потім будується функція . Якщо перший коефіцієнт дорівнює 1, у розрахунок приймається тільки перша функція. І так далі. Якщо цінність критеріїв однакова, коефіцієнти приймають значення по 0.5 при двох функціях.

Другим є метод послідовних поступок. Вирішимо спочатку задачу з єдиною цільовою функцією (У). Але отримане рішення може відрізнятися від максимуму рішення задачі з цільовою функцією (А). Пропонується зробити поступку в одному з рішень, тобто замість вимоги максимуму, наприклад (У), поставимо більш слабку вимогу відмінності нового экстремума від рішення задачі не більше ніж на 10%. У математичній формі ця вимога буде записано у формі нерівності:

0.9 х* < x < х*

Тоді одержимо однокритериальную задачу. Якщо рішення нас не влаштовує, процес поступок може продовжуватися. Підкреслимо ще раз, що величина поступок визначається обличчям, що приймає рішення.

Ще одним шляхом рішення цієї проблеми вибору є формування безлічі Парето. Переваги одного экстремума іншому можна віддавати, тільки якщо він за всіма критеріями краще другого. Якщо ж хоча б по одному з критеріїв, экстремум однієї цільової функції не гірше іншого, то дана крапка входить у Безліч Парето. Виділення безлічі дає підставу для встановлення нових принципів переваги.

Визначення обмежень і їх облік в процедурах оптимізації.

И3

Дата добавления: 2014-01-07