Пряма проектуюча

Пряма загального положення

Така пряма не паралельна і не перпендикулярна ні до однієї із площин проекцій (рис. 6).

Пряма рівня

Пряма рівня паралельна до однієї з площин проекцій (рис. 7).

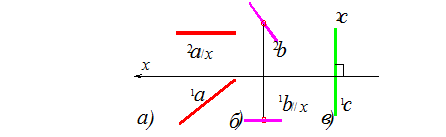
Рис. 7. Прямі рівня: а //¹П; b// ²П; с //³П: а –горизонтальна пряма; b –фронтальна пряма; с –профільна пряма

Проектуюча пряма перпендикулярна до однієї із площин проекції (рис. 8), де l ┴¹П; с ┴²П; q ┴³П.

Рис. 8. Проектуючі прямі: l – горизонтально–проектуюча;

с – фронтально–проектуюча; q – профільно–проектуюча

Висновки

Особливості проектуючи прямих та прямих рівня використовуються для спрощення розв’язків задач.

6. Сліди прямої

Слідами прямої називаються точки її перетину з площинами проекцій, при цьому:

– H –горизонтальний слід, наприклад H_а =а∩¹ П, тобто точка перетину прямої а з горизонтальною площиною;

– F –фронтальний слід, наприклад F_а =а∩² П, тобто точка перетину прямої а з фронтальною площиною;

– P –профільний слід, наприклад Р_а =а∩³ П, тобто точка перетину прямої а з профільною площиною.

Сліди прямої, як і будь–які точки, можна відобразити трьома проекціями.

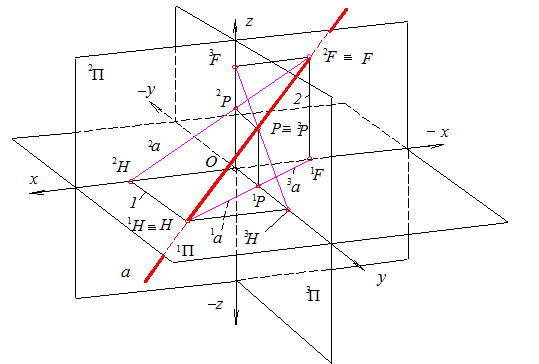
Рис. 9. Сліди прямої а в просторовій системі координат

Основні особливості слідів прямої:

–співпадання (тотожність) сліда із однією своєю ж проекцією, тобто Нι Н, F β F, Рγ P, що виникає внаслідок належності сліда до площини проекції;

–на відповідних проекціях прямої знаходяться проекції слідів із такими ж індексам.

На рис. 9 штриховими лініями зображено невидимі, закриті площинами проекцій, дільниці прямої а. Ця ж пряма а із слідами зображена на епюрі Монжа (рис. 10), де зберігаються описані вище властивості слідів. Римськими цифрами показані кути простору, через які проходять дільниці такої прямої.

Рис. 10. Сліди прямої та кути простору, через які вона проходить

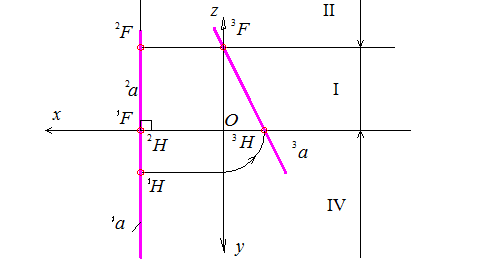
Рис. 11. Сліди профільної прямої

Проекції слідів прямої будуються за правилами побудови проекцій звичайних точок, використовуючи додаткові умови, тобто:

- перетин фронтальної проекції прямої з віссю x дає фронтальну проекцію горизонтального сліду ²Н, а перетин цієї ж проекції прямої з віссю z – фронтальну проекцію профільного сліду ² Р;

- перетин горизонтальної проекції прямої з віссю x дає горизонтальну проекцію фронтального сліду ¹ F, а перетин цієї ж проекції прямої з віссю у – горизонтальну проекцію профільного сліду ¹ Р;

- горизонтальна проекція горизонтального сліду ¹ Н знаходиться лінією зв’язку 1 на фронтальній проекції прямої;

- фронтальна проекція фронтального сліду ² F знаходиться лінією зв’язку 2 на фронтальній проекції прямої;

- інші проекції слідів знаходяться звичайним способом за відомими двома проекціями.

Для профільної прямої рівня межі октантів вказуються лініями, паралельними до осі z. Така пряма може мати тільки горизонтальний та фронтальний сліди (рис. 11).

Висновки

Сліди прямої використовуються в задачах на належність прямої до площини.

7. Дійсна величина відрізка прямої

Якщо відрізок прямої АВ є прямою загального положення, то дійсна величина відрізка не співпадає ні з однією із проекцій цього відрізка.

Дійсна величина відрізка АВ є гіпотенузою прямокутного трикутника, одним катетом якого є проекція відрізка на площину проекцій (будь–яку), а довжина другого катета дорівнює різниці відстаней кінців відрізка АВ від цієї ж площини проекцій.

На рис. 12 знайдена дійсна величина відрізка IАВI, використовуючи його горизонтальну проекцію ¹А¹В – в такому випадку IАВI=¹АВ₁ –, фронтальну проекцію ²А²В – тоді IАВI=²АВ₂ – та профільну проекцію ³А³В. Різниці відстаней кінців відрізка від площин ¹П, ²П, ³П, позначено як ∆z, ∆y, ∆x відповідно. Такий спосіб знаходження дійсної величини відрізка називають способом трикутника. Одночасно знаходиться дійсна величина кутів між прямою та площинами проекцій:

- α – між прямою та площиною ¹П;

- β – між прямою та площиною ²П;

- γ – між прямою та площиною ³П.

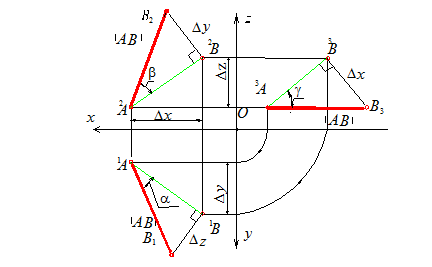
Рис. 12. Дійсна величина відрізка IАВI та кути між прямою l і площинами проекцій

Для прямих, паралельних до однієї із площин проекцій, дійсна величина відрізка дорівнює проекції відрізка на цю площину проекцій. Це часткоий випадок. який виникає із способу трикутника (рис. 12) при наявності однієї або двох із умов ∆x=0, ∆y=0, ∆z=0.

Висновки

Спосіб трикутника використовується у всіх метричних задачах.

8. Відносне розташування прямих

Дві прямі взаємно паралельні. якщо паралельні між собою одноіменні проекції цих прямих.

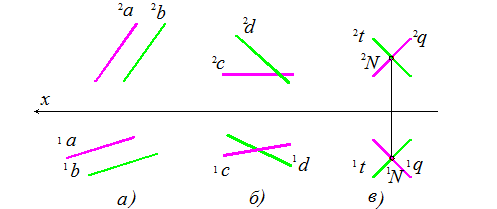
Рис. 13. Прямі: а – паралельні; б – мимобіжні; в – прямі. що перетинаються в точці N

Дві прямі перетинаються в точці N, якщо проекції цієї точки розташовані на одній лінії зв’язку, перпендикулярній до осі x (рис. 13, в).

Висновки

Інформація з цього питання використовується для аналізу задач.

Завдання на самопідготовку

Вивчити теоретичний матеріал лекції та засвоїти способи побудови проекцій елементів простору.

Література: [1], стр.6-20; [4].

Запитання для самоперевірки

1. Як задається пряма в просторі?
2. Що таке пряма загального положення?
3. Описати особливі положення прямої в просторі.
4. Що таке сліди прямої?
5. Як знаходяться сліди прямої?
6. Як знаходиться дійсна величина відрізка прямої?
7. Яким буває взаємне розташування прямих?
8. Як знаходиться дійсна величина кутів між прямою та площинами проекцій?
9. Чим відрізняється епюр Монжа від просторової декартової системи координат?
10. Як точка задається в просторі?
11. Як називаються площини проекцій?
12. Як знаходиться третя проекція точки?
13. Які три основні властивості епюра Монжа?

Висновки за обсягом лекції

Досконале знання всіх питань лекції необхідне для успішного вивчення матеріалу наступних лекцій.

Укладач доцент, к.т.н. Римар О.М.

Дата добавления: 2014-01-07