Формула Пуазейля. Примеры решения задач

Примеры решения задач

1. В широкой части горизонтальной трубы вода течет со скоростью . Определить скорость течения воды в узкой части трубы, если разность давлений в широкой и узкой ее частях равна

Решение:

Запишем уравнение Бернулли

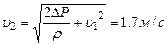
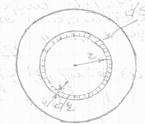
Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; самый близкий к трубе слой жидкости неподвижен.

Для установления зависимости 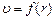выделим мысленно цилиндрический объем жидкости радиуса r и длины l. На торцах этого цилиндра поддерживаются давления P₁ и P_2, что обуславливает результирующую силу.

(1)

На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная

(2)

Где 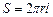- площадь боковой поверхности цилиндра.

F=F_тр (3)

Знак (-), так как 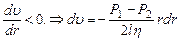(4)

Проинтегрируем это уравнение:

(5)

Наибольшую скорость имеет слой, текущий вдоль оси трубы (r=0):

Определим объемную скорость кровотока Q. Для этого выделим цилиндрический слой радиусом r и толщиной dr. Площадь сечения этого слоя 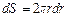. За 1с слой переносит объем жидкости (6)

(5)(6) получим (7)

(7) - Формула Пуазейля

Через трубу протекает тем больше жидкости, чем меньше ее вязкость и больше радиус трубы.

Формула Пуазейля аналогична закону Ома для участка цепи. Разность потенциалов соответствует разности давлений на концах трубы, сила тока - объемной скорости, электрическое сопротивление - гидравлическому сопротивлению

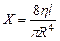(8)

Гидравлическое сопротивление тем больше, чем больше вязкость , длина l трубы и меньше сечение.

Дата добавления: 2014-01-07