Распределение Больцмана

Лекция 3

При рассмотрении распределения Максвелла полагалось, что внешние силовые поля отсутствуют. Рассмотрим случай, когда идеальный газ находится во внешнем силовом поле. Рассмотрим модельный вариант.

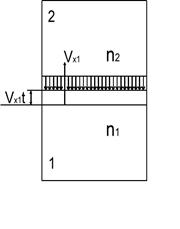Пусть дан сосуд. В нем находится газ, который разделен на две части – 1 и 2, между которыми действует силовое поле.

Допустим, что в начальный момент времени число молекул было одинаковым в обеих половинках. Объемы тоже одинаковы. Следовательно, концентрации также равны.

Однако, из-за действия силового поля количество молекул, переходящих из второй области в первую за единицу времени будет превышать число молекул, переходящих из первой области во вторую. В результате концентрация молекул в первой области будет возрастать, а во второй – убывать. В итоге число молекул, переходящих из области 2 в область 1 начнет снижаться, а обратный поток увеличится.

Таким образом, через определенный промежуток времени потоки выровняются, и концентрация в областях перестанет изменяться. В конечном итоге в первой области будет концентрация 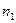, во второй области - 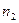. В таком равновесном состоянии система будет находиться как угодно долго. Нашей задачей является установить связь между этими установившимися концентрациями.

Выделим в первой области молекулу со скоростью 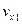(ось направим вертикально вверх). Предполагается, что молекула находится недалеко от границы и через небольшой промежуток времени достигает её и переходит во вторую область. Выделим соответствующий объёмчик высотой . Будем считать, что он цилиндрический с основанием 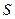. Тогда

.

Число молекул попадающих в этот объем и имеющих проекции скорости 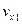обозначим через 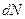. Все они переходят во вторую область. Тогда

,

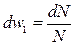где 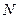– число молекул в этом объеме, .

.

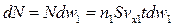Пусть 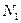- число молекул, переходящих из первой области во вторую за некоторый достаточно малый промежуток времени

.

Проводя аналогичные рассуждения для молекул, переходящих из второй области в первую можно записать, что

.

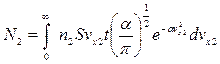Так как система находится в состоянии равновесия, то 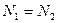. Значит, эти интегралы можно приравнять

,

.

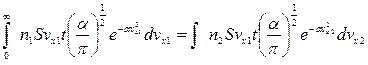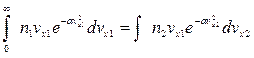Обозначим потенциальную энергию, которую приобретает молекула при переходе из первой области во вторую через 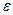. Тогда можем записать, что

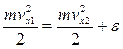(2).

(Состояние равновесия не нарушится, если при переходе из первой области во вторую молекула 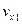превращается в молекулу , и наоборот).

Возьмем дифференциалы от обеих частей выражения (2)

,

.

Сравним наши интегралы. Если , то .

Выразим 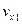из (2)

.

Тогда:

,

.

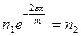Подставляя выражение для окончательно получим

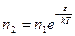(3).

Полученное соотношение (3) называется законом распределения Больцмана.

В более общем смысле

(3^’),

где -потенциальная энергия, которая соответствует области .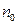

Воспользуемся формулой 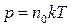. Выразим 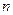и подставим в (3’)

,

,

/

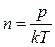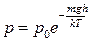В виде следствия получили формулу, которая носит название барометрической.

Дата добавления: 2014-01-07