Динамический анализ

Алгоритм обследования.

Показания к РКТ – выявленные при УЗИ очаговые образования печени, выявленные при УЗИ очаговые образования поджелудочной железы, подозрения на рубцовые изменения в проекции желчного пузыря, высказанное по результатам УЗИ, дифференциальная диагностика причин механической желтухи.

Предварительная подготовка к РКТ – накануне исследования (на ночь) 7-10 мл водорастворимого контрастного вещества (омнипак), разведённого в стакане воды; за 1-1.5 часа до исследования повторный приём той же дозы контрастного вещества.

Контрастное усиление – внутривенное введение 40-80 мл 60-76% раствора контрастного вещества.

1. Всем больным на первом этапе обследования выполняют УЗИ.
2. При ультразвуковых признаках очаговых образований печени и поджелудочной железы, получении недостаточной информации о состоянии поджелудочной железы на втором этапе обследования используют РКТ с целью уточнения характера изменений.
3. При ультразвуковых признаках биллиарной гипертензии, наличии у больных эпизодов желтухи в анамнезе на втором этапе обследования проводят ЭРХПГ.

На практике изменение набора входных переменных комбинационной схемы часто происходит при несогласованных во времени изменениях различных входных переменных. При этом схема фактически находится под действием нескольких последовательно сменяющихся наборов, причем каждый из них дробится еще на несколько наборов при прохождении через схему из-за несогласованных значений t_зд.ср. элементов. В результате реально изменение сигнала на каждом выходе схемы и внутреннем узле происходит не мгновенно, а образует сложный динамический процесс. Нахождение таких процессов называется динамическим анализом комбинационной схемы.

Динамический анализ ведется с учетом следующих обстоятельств.

1. Изменение входного набора схемы состоит из неодновременных изменений различных входных переменных, образующих этот набор. Поэтому последовательность входных наборов можно рассматривать как набор входных последовательностей из нулей и единиц, действующих независимо друг от друга на разных входах.

Переключательным процессом называется последовательность уровней "1" и "0" (импульсов и пауз), которая на любом конечном наблюдаемом интервале времени содержит конечное число переходов 01 и 10. Примеры переключательных процессов приведены на рис. 2.

Длина переключательного процесса - это общее число изменений сигнала в нем. Например, для процесса x₄ на рис.2 длина равна 3. Переключательный процесс называется сложным, если его длина больше или равна 2. В противном случае он называется простым переключением.

Для векторного процесса (переключения совокупности переменных) соответствующим понятием является вектор длин. Компоненты этого вектора - длины процессов, являющихся компонентами векторного процесса. Например, векторный процесс, компонентами которого являются шесть процессов на рис. 2, имеет вектор длин (5, 3,1,1,0,0). Векторный переключательный процесс считается простым переключением, если все его компоненты – простые переключения, совершаемые одновременно. В противном случае векторный процесс считается сложным. На рис.2 набор (вектор) X₁ = х₅ x₄ x₃ x₂ x₁ x₀ = 101010 изменяется на набор (вектор) X₂ = 010110.

Рис.2

СТАТИЧЕСКИЕ РИСКИ СБОЯ

На рис. показана работа элементов И и ИЛИ при подаче на их входы двух последовательных во времени наборов X1 = х1x0 =01 и Х2= х1x0 = 10. Значение сигнала у1 для элемента И на этих наборах должно оставаться постоянным и равным 0, а у2- равным 1. Это выполняется для случаев разброса во времени моментов переключения переменных х1 и x2, показанных на рис. а и г. Если же этот разброс соответствует рис. б и в, то видно, что на выходе схемы И появится логический сигнал 1 длительностью дельта r1, а на выходе схемы ИЛИ - сигнал 0 длительностью дельта r2. Эти ложные сигналы и являются рисками сбоя, причем видно, что они могут быть, а могут и отсутствовать.

Все дальнейшие примеры будут иллюстрироваться временными диаграммами для наихудшего случая, когда риск сбоя обязательно имеет место.

Риск сбоя называется статическим, если у(Х1) = у(Х2), где у - булева функция. Риск сбоя называется статическим в нуле S0, если у(Х1) = у(Х2) = 0. Риск сбоя называется статическим в единице S1, если у(Х1) = у(Х2) = 1.

Итак, на рис. 6, б имеет место статический риск сбоя в нуле S0, а на рис. в - статический риск сбоя в единице S1.

Существенно, что полученные помехи S0 и S1 (иногда их называют иголками, мерцаниями, глитчами (от англ. glitch) - это короткий всплеск напряжения малой амплитуды, которым нельзя пренебрегать. При достаточно большой разности Dt помеха будет иметь длительность, во много раз превышающую время переключения элемента, и амплитуду, равную номинальному сигналу. Это уже полноценный сигнал, на который могут реагировать последующие элементы (входы синхронизации, установки в 0 или 1, загрузки данных и т. п.). Такие помехи - страшная вещь для цифровых схем, тем более что их практически невозможно увидеть на осциллографе, и разработчик просто не будет знать об их существовании. Они могут сужаться до полного исчезновения, но могут и расширяться, проходя через логические цепи.

ДИНАМИЧЕСКИЕ РИСКИ СБОЯ

На рис. а приведена схема, реализующая функции у = х2х1+х0.

Пусть входной набор X1 = х2x1x0 = 010 изменяется на входной набор X2 = х2х1х0 = 101. На рис. 7, б приведены временные диаграммы, соответствующие наихудшему случаю разброса моментов переключения переменных x2, x1 и x0. Поскольку у(Х1) = 0, а у(Х2) = 1, из рис. 7, б видно, что на выходе схемы многократное переключение вместо идеального алгоритмического перехода 01. Пусть входной набор X1 = х2х1х0 = 011 изменяется на входной набор X2 = х2x1x0 = 100. Из рис. 7, в видно, что вместо идеального алгоритмического перехода 10 на выходе многократное переключение.

Риск сбоя называется динамическим, если у(Х1) <> у(Х2), где у- булева функция. Риск сбоя называется динамическим D₊ при переходе на выходе 01, если у(Х1) = 0, а у(Х2) = 1. Риск сбоя называется динамическим D_-, если у(Х1) = 1, а у(Х2) = 0. Итак, на рис. 7, б имеет место динамический риск сбоя D₊, а на рис. 7, в – D_-. Из временных диаграмм работы схемы видно, что динамический риск сбоя является следствием статического риска сбоя. Наличие динамических рисков сбоя в цифровой схеме также может привести к нарушению закона ее функционирования.

ЛОГИЧЕСКИЙ РИСК СБОЯ

Рассмотрим переход от X1 = х2х1x0 = 110 к X2 = х2х1x0 = =010 для функции у, представленной картой Карно (рис. 8, а). Для нее можно записать у = х2x1 +~х2~x0. На рис. б приведена соответствующая схема.

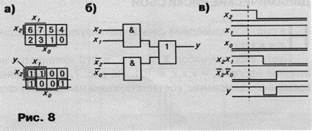
Обратите внимание, что в данном случае осуществляется переход между соседними наборами, причем х1 = 1 и х2= 0 являются константными сигналами, следовательно, для функции можно записать в данном случае у = х2 + ~х2. Ясно, что здесь у(Х1) = у(Х2) = 1, однако мы видели (см. рис. 6, в), что на элементе ИЛИ возможен статический риск сбоя в единице. Это отражено на рис. в.

Попытаемся устранить этот риск сбоя, видоизменив аппаратную реализацию данной функции. Введем в карте Карно дополнительный контур, показанный штриховой линией, тогда уравнение для функции будет иметь вид у = х2x1 + ~x2~x0 + x1~x0 (рис. 9, а). Так как при переходе от набора X1 к X2 простая импликанта х1~х0 все время равна 1, то риск сбоя, выявленный выше, не будет проявляться на выходе схемы. Эта ситуация отражена на временной диаграмме, представленной на рис. 9, б.

Статический риск сбоя, проявляющийся при соседней смене наборов, называется логическим, так как может быть устранен изменением логической структуры, реализующей булеву функцию.

ФУНКЦИОНАЛЬНЫЙ РИСК СБОЯ

Рассмотрим теперь поведение выходного сигнала той же функции при многоместной смене наборов. Пусть набор 0 переходит в набор 7. Так как все переменные изменяются, а моменты их изменения в общем случае неизвестны, то возможны различные переходы от набора 0 к набору 7 (см. рис. 10, а). Есть единственный путь смены наборов: 0->2->6->7, при котором не будет статического риска сбоя, так как у(Х1=0) = у(Х2=7) = 1. Во всех остальных случаях будет статический риск сбоя в единице S1, причем никакими аппаратными средствами устранить его нельзя, так как значения выхода на промежуточных наборах определяются характером самой функции.

По тем же причинам при переходе от набора X1 = 1, на котором у(Х1) = 0, к набору X2 = 6, на котором у(Х2) = 1, возможен путь смены наборов: 1 ->0->4->6, когда имеет место динамический риск сбоя D₊, также определяемый характером самой функции. Во всех остальных случаях смены наборов будет чисто алгоритмический переход 01 (см.рис. 10, б).

Риски сбоя, проявляющиеся при многоместной смене наборов и определяемые характером самой функции, называются функциональными. Такие риски сбоя не могу быть устранены изменением логической структуры, реализующей булеву функцию.

Лекция №2

МЕТОДЫ АНАЛИЗА КОМБИНАЦИОННЫХ

СХЕМ НА РИСКИ СБОЯ

Анализ логических схем будем рассматривать как процедуру выявления рисков сбоя из-за различного вида состязаний сигналов, то есть процедуру оценки функциональной устойчивости схем.

В настоящее время разработано большое количество методов анализа комбинационных схем на риски сбоя. Рассмотрим два из них, которые относятся к методам использования многозначной логики: метод трехзначного моделирования и метод восьмизначного моделирования.

МЕТОД ТРЕХЗНАЧНОГО МОДЕЛИРОВАНИЯ

Так как логическая функция задается для троичного моделирования в виде системы булевых уравнений, необходимо определить троичные функции выходов основных булевых элементов НЕ, И, ИЛИ.

В табл. 1 приведены выходные сигналы для основных логических элементов, на входах которых действуют трехзначные сигналы.

При трехзначном моделировании значение функции определяется не только для наборов X1 и X2, но и для переходного вектора Х1/Х2, задающего состояние схемы во время переходного процесса.

Пусть на схему, имеющую n входов, последовательно подаются два входных набора X1 = а_n-1,..., а_j,..., а₀ и X2 = b_n-1,...,b_j, …,b₀. Тогда переходный вектор Х1/Х2 имеет следующий вид:Х1/Х2= c_n-1, …, с_j,..., c₀, где с, = 1/2, если а_j <> b_j, и с_j == а_j, если а_j= b_j, при j =0, 1, 2,..., n-1.

Если при моделировании для некоторых последовательных наборов X1 и Х2 зафиксировано, что у(Х1) = у(Х2), а у(Х1/Х2) = 1/2, то схема содержит статический риск сбоя.

Проанализируем работу схемы, которая реализует функцию у = x3~x2 +x3~x0 + ~x3x2x0 + ~x2x1~x0 для следующих переходов: 14->8; 1->10; 0->13; 12->1; 6->8. Результаты моделирования приведены в табл. 2. Для перехода 14->8 выявлено, что у = 1 на обоих наборах и на переходном векторе, несмотря на наличие S₀ на выходе элемента, реализующего простую импликанту ~x2x1~x0. При переходе 1->10 на выходе схемы имеет место чисто алгоритмический переход 01. Для перехода 0->13 выявлен статический риск сбоя в нуле S₀. При переходе 12->1 на выходе схемы на переходном векторе обязательно будет сигнал 1/2, так как у(Х1=12) = 1, а у(Х2=1) = 0. Динамический риск сбоя на выходе может проявиться только при наличии статических рисков сбоя на промежуточных сигналах. В нашем случае на простых импликантах x3~x2 и ~x3x2x0 на переходном векторе обнаружен S₀, а на импликанте х3~х0 чистый переход 10, следовательно, на выходе в наихудшем случае возможен динамический риск сбоя D_-. Аналогично при переходе 6->8 обнаруживается динамический риск сбоя D₊.

Из приведенных примеров видно, что по методу трехзначного моделирования в явном виде обнаруживаются только статические риски сбоя в комбинационных схемах.

Динамический риск сбоя определяется как следствие статического в промежуточной цепи схемы. Метод трехзначного моделирования особенно эффективен для анализа последовательностных схем и широко применяется в практике.

МЕТОД ВОСЬМИЗНАЧНОГО МОДЕЛИРОВАНИЯ

При восьмизначном моделировании для представления значений величин сигналов берется множество L = {1,0, +, -, S₁, S₀, D₊, D_-}. В табл. 3 приведены выходные сигналы для основных логических элементов на входах которых действуют восьмизначные сигналы. Несколько примеров реакции элементов И и ИЛИ на восьмизначные сигналы для наихудшего случая приведены на рис. 1.

Проанализируем работу той же схемы и для тех же переходов, которая была рассмотрена в предыдущем разделе. Результаты моделирования приведены в табл. 4, из которой видно, что восьмизначное моделирование в явном виде определяет и статические, и динамические риски сбоя.

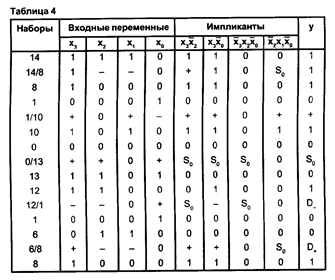
Рассмотренный метод нагляден, удобен, применим и для ручного, и для машинного анализа.

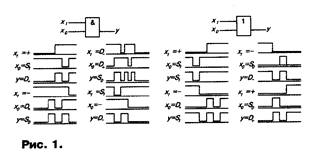
Лекция 3

РЕКОМЕНДАЦИИ ПО УСТРАНЕНИЮ РИСКОВ СБОЯ

В КОМБИНАЦИОННЫХ СХЕМАХ

Все методы, разработанные для устранения рисков сбоя в комбинационных схемах, можно объединить в три группы:

· структурные;

· функциональные;

· конструктивно-технологические.

Структурные методы направлены на получение необходимых свойств реализации устройства при неизменном алгоритме его работы.

Функциональные методы связаны с изменением алгоритма работы, в частности кодирования состояний входов.

Конструктивно-технологические методы ориентированы на получение требуемых ограничений на уровне используемых математических моделей.

Наиболее простыми для соответствующей математической модели являются структурные и функциональные методы, а наиболее сложными - конструктивно-технологические, так как они часто связаны с разработкой принципиально новых видов производства интегральных цифровых схем.

Структурные методы

Как отмечалось в разделе "Логический риск сбоя" [1], при соседней смене входных наборов в комбинационных схемах могут быть устранены статические риски сбоя. В общем случае одной из основных задач синтеза комбинационных схем, свободных от статических рисков сбоя и представленных в дизъюнктивных нормальных формах (ДНФ), будет отыскание таких минимальных покрытий единичных клеток ФАЛ в карте Карно импликантами (контурами на картах Карно), в которых любые соседние единичные клетки покрыты, по меньшей мере, одной импликантой (контуром).

Аналогично для функции, представленной в конъюнктивной нормальной форме (КНФ), необходимо найти такое минимальное покрытие нулевых клеток карты Карно, в котором любые две соседние нулевые клетки покрыты, по крайней мере, одним контуром.

На рис. 1 показаны карты Карно для функций, свободных от статических рисков сбоя S1, при переходах между любыми соседними единичными клетками. Функция в случае а) не требует дополнительных импликант, так как все смежные контуры покрыты другими контурами, а в случаях б) и в) введены контуры, показанные штриховой линией.

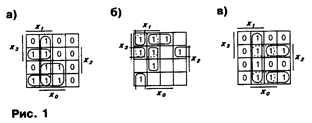
Отметим, что в рассмотренных случаях можно получить и скобочные формы функций, и формы с групповой инверсией, которым также будут соответствовать схемы, свободные от S1. Если же допускаются несоседние изменения входных наборов, то в общем случае невозможно синтезировать комбинационные схемы, свободные от рисков сбоя (см. раздел "Функциональный риск сбоя" в [1]).

Иногда в схемы вводят задержки таким образом, чтобы гарантировать, что цепь не будет проходить через какой-либо промежуточный набор, требующий изменения значения функции. Однако это не устранит сбоев при обратном переходе. Часто используют введение в схему максимальных инерционных задержек, еще не нарушающих алгоритма работы схемы. К сожалению, такой способ не позволяет изменять в случае необходимости частоту работы схемы, например при переходе в турборежим. Часто рисков сбоя можно избежать, если использовать ранний сигнал для включения (выключения) элемента, установленного в цепь распространения позднего сигнала. Несложно предложить и другие формы использования сведений о минимально возможной задержке или о наибольшей возможной кратности максимального и минимального значений задержки. Полезны противогоночные схемы, построенные так, что в них, если и возникают, то только неопасные гонки, то есть такие, при которых отсутствует риск появления на выходе сигналов, не предусмотренных логическим выражением (законом функционирования).

Примером неопасной гонки может служить гонка фронта по нескольким трактам с последующим объединением на выходе элемента: какой бы фронт ни выиграл гонку, результат все равно будет верный, изменится лишь задержка его получения.

Причиной риска сбоя может быть неправильно спроектированная схема. Таким примером является генератор двухфазной системы синхронизации (рис. 2, а). Здесь комбинационная схема представлена двумя вентилями_И, на выходах которых реализуются уравнения: Ф1= QT;' Ф2 = ~QT.

Задержка переключения триггера в данном случае приводит к появлению статических рисков сбоя S0 на выходе Ф1 при переходе с набора QT = 10 на набор QT = 01 и на выходе Ф2 при переходе с набора ~QT = 10 на QT= 01. Устранить эти сбои можно двумя схемотехническими (структурными) методами.

На рис. 2, б комбинационная схема выполнена на вентилях ИЛИ. Из соответствующих временных диаграмм видно, что в этом случае риски сбоя не появляются. Выходные сигналы Ф1 и Ф2 при необходимости можно инвертировать. На рис. 2, в оставлены вентили И, а D-триггер заменен на JK-триггер, срабатывающий по переходу 10 на его тактовом входе. Временные диаграммы показывают на отсутствие в данной схеме рисков сбоя.

Наиболее универсальными и поэтому широко используемыми методами борьбы с рисками сбоя являются тактирование и стробирование. Суть тактирования заключается в следующем. По всему цифровому устройству разводится единая система тактирующих (синхронизирующих) сигналов, обеспечивающих запись информационных данных в регистры через интервал времени, превышающий самый длинный процесс неопределенности, то есть самую большую задержку во всех трактах схемы. Если же необходимо лишь очистить сигнал от рисков сбоя, а не запомнить его, то используется метод стробирования, реализуемый соответствующим построением комбинационной схемы.

Достоинство тактирования и стробирования в том, что разработчику не требуется вникать в специфику протекания переходных процессов, в характер возникающих гоночных ситуаций и т. д. Все, что должен знать разработчик, это максимально возможная задержка самого длинного тракта логической схемы, а это легко вычисляется по паспортным данным используемых элементов.

На рис 3, а приведена схема преобразователя однофазного сигнала в четырехфазный. Комбинационная схема здесь - дешифратор с активным нулем на его выходах. Входными переменными для дешифратора являются выходы триггеров двухразрядного счетчика с последовательным переносом. Как видно из временных диаграмм (рис. 3, б), на выходах y0 и у2 дешифратора имеет место статический риск сбоя S1. Использование синхронного двухразрядного счетчика не устранит его, а в лучшем случае уменьшит длительность паразитных сигналов.

На рис. 4 показано использование метода стробирования (в качестве стробирующего применяется тактовый сигнал), а на рис. 5 - метода тактирования для устранения рисков сбоя. Полезно помнить, что апробирование осуществляется комбинационной схемой - при этом деформируется длительность информационного сигнала, а тактирование – последовательностной схемой, сдвигающей информационный сигнал во времени.

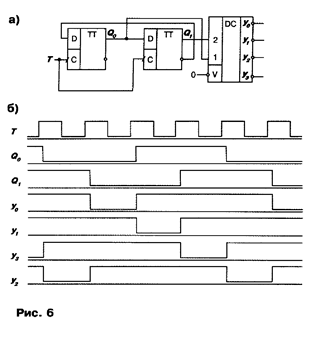
Пример функционального метода устранения рисков сбоя приведен на рис. 6. Здесь используется принцип изменения кодирования последовательных состояний входов комбинационной схемы. В схеме рис. 6, а счетчик изменяет свои состояния не в естественной двоичной последовательности 0-1-2-3, а в последовательности 0-1-3-2, когда в каждом такте изменяется состояние только одного разряда счетчика (здесь используется двухразрядный счетчик Джонсона - сдвиговый регистр с одной перекрестной связью). Из рис. 6, б видно, что в данном случае риски сбоя на выходах дешифратора отсутствуют.

Растет интерес к еще одному методу борьбы с гонками - самосинхронизирующимся схемам [2]. Рабочие узлы в этом случае строятся не противогоночными, а дополняются специальными схемами, обнаруживающими факт окончания переходных процессов и вырабатывающими сигнал разрешения для следующих схем, который в каком-то смысле играет роль асинхронного синхросигнала. Это направление весьма перспективно для построения БИС и особенно СБИС, где применение обычной синхронизации встречает ряд трудностей. Однако в схемах и микросхемах малой степени интеграции и традиционной технологии оно пока не находит применения ввиду сложности построения такого рода схем и удвоения аппаратурных затрат.

К конструктивно-технологическому методу можно отнести метод борьбы с влиянием входных гонок на уровне одного логического элемента, основанный исключительно на совершенствовании технологии его изготовления и конструктивного исполнения, что в совокупности должно обеспечить минимальные разбросы задержки распространения сигналов в элементе по логически одинаковым цепям. В частности, использование интегральной технологии производства ИС, позволяющей получать весьма малые относительные вариации различных параметров, дает возможность считать, что гонки по входу практически не влияют на устойчивость цифровых устройств, проектируемых на любой серии логических ИС.

Полезно придерживаться также следующих рекомендаций:

· соблюдать требования технических условий на ИС;

· при проектировании аппаратуры уделять особое внимание рациональной разводке печатных плат;

· обеспечивать режимы эксплуатации, не изменяющие задержки распространения сигналов (стабилизацию источников питания, термостатирование, буферизацию нагрузок и др.).

Дата добавления: 2014-01-07