Понятие множества. Основные понятия языка

Основные понятия языка.

ЯЗЫК – знаковая информационная система, выполняющая функции кодирования, хранения и передачи информации.

Знак – это представитель (заместитель) обсуждаемого объекта.

Знаки бывают языковые и неязыковые. К неязыковым знакам относятся: знаки – индексы (дым, как знак горения; t^o С тела, как знак здоровья и т.п.); знаки – сигналы (звон, стук, свист и т.п.); знаки – копии (фото, отпечатки пальцев и т.п.).

Логика изучает языковые знаки. Для обозначения объектов с их помощью служат имена.

Имя – это слово или словосочетание, обозначающее какой-либо объект или группу объектов.

Как правило, имена имеют значение и обязательно смысл.

Значение имени (денотат, номинат) – это объект, названный данным именем. Под объектом необходимо понимать вещь или явление, например, действие или бездействие.

Значение из множества других выделяется с помощью ощущений.

Смысл имени (концепт) – это информация об объекте, позволяющая однозначно выделить его из ряда других. Языковые выражения, лишенные смысла, не являются именами, т.е. ничего не обозначают.

Пример: имя – Луна. Значение этого имени видим ясным вечером на небе. Смысл – естественный спутник Земли. Имя – стук. Значение этого имени слышим. Смысл – звуковые колебания воздуха низкой частоты.

Имена могут обозначать объекты, которые не существуют в действительности. Такие имена называются мнимыми (вечный двигатель, русалка и т.п.). Кроме того, имена по денотату бывают единичными и общими, т.е. обозначающими единичный объект или являющиеся общими для нескольких объектов.

Роль знаков в языке исследовали многие мыслители, начиная с Аристотеля. Но особенно актуальными эти проблемы стали в 19 веке в связи с развитием науки о языке.

Американский философ Ч. Пирс заложил основы особой науки о знаках – семиотики. В этой науке выделяют три раздела – синтаксис, семантику и прагматику.

Синтаксис – исследования отношений между самими знаками, т.е. правила построения и преобразования выражений языка.

Семантика – исследования отношений знаков к представляемым ими объектам, т.е. смыслы знаков. Пример: «животное» от слова «живот», «жизнь».

Прагматика изучает отношение человека к знакам, а также отношения между людьми в процессе знакового (языкового) общения. Здесь речь идет об эмоциональных, эстетических, экономических и других отношениях. (Например, как сказать: воняет или пахнет? Врет или ошибается? Здесь можно отметить проблемы переименования объектов.)

Как и другие науки, логика оперирует собственными понятиями.

Одним из исходных понятий языка логики является понятие «множество».

Множество – это такая совокупность единичных объектов, в которой каждому объекту присущи одни и те же свойства. Отдельные объекты множества – это элементы.

Например, множество А = {1, 2, 5, 8, 4}состоит из чисел, порядок вхождения которых безразличен. В таком случае, каждое из чисел является элементом множества А, т.е. включено в него: 1 Î А, 2 Î А... и т.д.

Иногда порядок расположения элементов множества фиксируется. Такое множество называется упорядоченным или кортежем: В = <1, 2, 3, 4, 5>.

Если имеется множество С = {1, 8, 4,}, тогда С есть правильная часть множества А или его подмножество С Ì А.

Д = {8} – единичное множество. Е = { }= Ø – пустое множество.

Существует два способа задания множеств: экстенсиональный и интенсиональный.

Экстенсиональный (количественный) способ задает множество путем перечисления всех его элементов. Так, элементами множества А являются числа 1, 2, 5, 8, 4. Очевидно, что так можно задать только конечные и при этом очень небольшие множества.

Интенсиональный (качественный) способ, напротив, предназначен для задания больших и даже бесконечных множеств. Этот способ состоит в указании какого-либо свойства, общего для всех элементов данного множества. Например, множество всех граждан России определяется как множество всех людей, обладающих свойством гражданства России. Тогда для каждого человека легко определить, будет ли он элементом данного множества, уточнив, обладает ли он гражданинством России. Пример бесконечного множества – множество всех чисел, т.е. множество всех объектов, обладающих свойством – быть числом. Бесконечные или очень большие множества широко применяются в науке (математика, социология и др.).

Основные отношения между множествами:

1) отношение включения (подчинения);

2) отношение эквивалентности (тождества);

3) отношение пересечения;

4) отношение внеположенности (несовместимости).

Отношения между множествами удобно отображать с помощью геометрических фигур, которые предложил Л. Эйлер. Леонард Эйлер (1707–1783) – швейцарец по происхождению, выдающийся русский математик и естествоиспытатель. Круги, носящие его имя, были изобретены им именно для наглядной иллюстрации отношений между множествами. В этих кругах каждая точка представляет один элемент множества.

Изобразим названные отношения с помощью кругов Эйлера.

1) Пусть А = {1, 2, 5, 8, 12} и В = {1, 2, 8} тогда

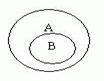
т.е. множество В есть подмножество множества А – отношение включения: ВÌА.

2) Пусть А = {1, 2, 5, 8, 12} и В = {1, 5, 2, 12, 8}, т.е. оба множества состоят из одних и тех же элементов (порядок расположения элементов в множестве не играет роли). В этом случае А и В есть всего лишь разные имена для обозначения одного и того же множества. При попытке совмещения кругов, обозначающих эти множества, они сливаются и становятся неразличимыми – отношение эквивалентности.

3) Пусть А = {1, 2, 5, 8, 12} и В ={1, 2, 5, 13, 18}, тогда

т.е. общие элементы обоих множеств (1, 2, 5) попадают в заштрихованную часть кругов, а незаштрихованные области А и В содержат несовпадающие элементы (для А это 8 и 12, а для В – 13, 18) – отношение пересечения.

4) Пусть А = {1, 2, 5, 8, 12} и В = {3, 4, 7, 9, 11}, т.е. множества А и В не имеют ни одного общего элемента, тогда

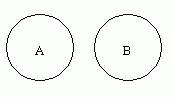
– отношение внеположенности (несовместимости).

Все подмножества одного и того же множества состоят к нему в отношении включения и подчинения. Для любых двух подмножеств множества отношения между собой могут быть совместными, т.е. совпадающими по объему, или несовместными.

Отношения между подмножествами (деление по объему)

Объемы подмножеств по количеству элементов могут быть одинаковы, но о тождестве подмножеств идет речь, когда все элементы одни и те же! Если же при равном количестве элементов некоторые не совпадают, то тождество исчезает и возникает пересечение объемов подмножеств. При разном количестве элементов тождество невозможно. В лучшем случае будет отношение пересечения объемов подмножества.

Когда же не совпадает ни один элемент, возникает внеположенность объемов подмножеств, т.е. несовместимость по отношению друг другу.

Отношение множеств мы используем при анализе понятия как формы абстрактного мышления.

Дата добавления: 2014-01-07