Вычитание

Сложение

Арифметические операции над двоичными кодами

Сложение двоичных кодов производится побитно на основе следующих соотношений: 0+0=0; 0+1=1; 1+0=1; 1+1=0 и 1-в перенос (в результате 10).

Например:

1 перенос 111 переносы
₊9 ₊1001 ₊7 ₊0111
5010110001
14 1110 8 1000

Это действие можно выполнять так же как и в десятичных кодах, занимая 1 старшего разряда (производить заем):

1 заем
_- 10 _-1010

50101
5 0101

Но для многоразрядных кодов процедура очень осложняется, когда приходится занимать не из соседнего старшего разряда а из более старших разрядов. Поэтому в цифровой технике вводится понятие дополнительного кода, который позволяет совершенно одинаково выполнять операции сложения и вычитания. Для указания знака кода используется самый старший его разряд. В положительном коде старший разряд равен нулю, а в отрицательном – единице. Дополнительный код положительного числа совпадает с его прямым (обычным) кодом. Дополнительный код отрицательного числа получается путем инверсии прямого кода и добавления к результату единицы.

Например: прямой и дополнительный код числа +5 равен 0101, дополнительный код числа –5 равен 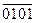+1=1010+1=1011.

Старший разряд “1” указывает, что код представляет отрицательное число. Код называется дополнительным потому, что он дополняет n-разрядный прямой код до значения 2ⁿ.В приведенном примере 0101+1011=10000₂=2⁴_.

Имеется другой способ определения дополнительного кода,несколько быстрее приводящий к цели. Разряды прямого кода переписываются справа налево, начиная с младшего разряда D₀ до первой встретившейся 1,остальные разряды инвертируются.

Например 10110_пр=01010_доп.

Вычитание двоичных кодов сводится к сложению положительных и отрицательных кодов и выполняется как сложение их дополнительных кодов. При выполнении этой операции очень важно проследить чтобы результат действия над кодами не исказил знаковый разряд. Поэтому должен быть определенный запас нулевых разрядов, расположенных после знакового разряда. В нижеприведённых примерах операнды занимают всего 4 разряда,но будем использовать восьмиразрядные коды.

Рассмотрим различные ситуации при вычитании.

1) Вычислим в двоичных кодах результат операции 7-5=7+(-5)
Определим дополнительный код –5=-00000101_пр=11111011_доп.
Тогда 7₁₀-5₁₀=00000111_доп[phone]_доп=1.00000010_доп=00000010_пр=2₁₀

Возникший перенос 1 в разряд D₈ отбрасывается. Знаковый разряд D₇=0,поэтому результат – положительное число 2,у которого прямой код такой же,как и дополнительный.

2) Определим результат операции 5₁₀-7₁₀=
=00000101_пр-00000111_пр=00000101_доп[phone]_доп=11111110_доп=-00000010_пр=-2₁₀
ЗдесьD₇=1,результат отрицательный, поэтому дополнительный код переводится в прямой. Это выполняется по тому же правилу,что и перевод прямого кода в дополнительный.

3) Найдём –5₁₀-7₁₀=11111011_доп[phone]_доп=1.11110100_доп=- 00001100_пр=-12₁₀.

Дата добавления: 2014-01-07