ТЕМА 9. Шифраторы и дешифраторы. Сумматоры и полусумматоры

9.1 Шифраторы, дешифраторы и преобразователи кодов

Шифратор — это комбинационное устройство, преоб­разующее десятичные числа в двоичную систему счисле­ния, причем каждому входу может быть поставлено в соот­ветствие десятичное число, а набор выходных логических сигналов соответствует определенному двоичному коду. Шифратор иногда называют «кодером» (от англ. coder) и используют, например, для перевода десятичных чисел, набранных на клавиатуре кнопочного пульта управления, в двоичные числа. Если количество входов настолько ве­лико, что в шифраторе используются все возможные ком­бинации сигналов на выходе, то такой шифратор называ­ется полным, если не все, то неполным. Число входов и выходов в полном шифраторе связано соотношением n = 2^m, где n — число входов, m — число выходов. Так, для пре­образования кода кнопочного пульта в четырехразрядное двоичное число достаточно использовать лишь 10 входов, в то время как полное число возможных входов будет рав­но 16 (n = 2⁴ = 16), поэтому шифратор 10x4 (из 10 в 4) будет неполным.

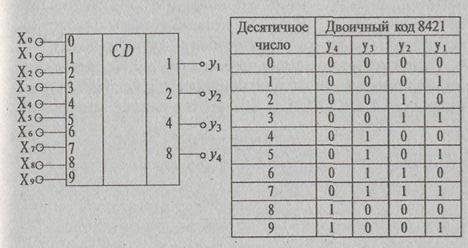
Рассмотрим пример построения шифратора для преоб­разования десятиразрядного единичного кода (десятичных чисел от 0 до 9) в двоичный код. При этом предполагает­ся, что сигнал, соответствующий логической единице, в каждый момент времени подается только на один вход. Условное обозначение такого шифратора и таблица соот­ветствия кода приведены на рис. 3.61. Используя данную таблицу соответствия, запишем логические выражения, включая в логическую сумму те входные переменные, ко­торые соответствуют единице некоторой выходной пере­менной. Так, на выходе у, будет логическая «1»тогда, когда логическая «1» будет или на входе X,, или Х3, или Х5, или Х7, или X,, т. е.

У₁ = X₁ + Х₃ + Х₅ + Х₇ + X₉.

Аналогично получаем

У₂ = X₂ + X₃ + X₆ + X₇

У₃ = X₄ + X₅ + X₆ + Х₇, у₄ = Х₈+ Х₉.

Представим на рис. 3.62 схему такого шифратора, ис­пользуя элементы ИЛИ.

На практике часто используют шифратор с приорите­том. В таких шифраторах код двоичного числа соответ­ствует наивысшему номеру входа, на который подан сигнал «1», т. е. на приоритетный шифратор допускается по­давать сигналы на несколько входов, а он выставляет на выходе код числа, соответствующего старшему входу.

Рассмотрим в качестве примера (рис. 3.63) шифратор с приоритетом (приоритетный шифратор) К555ИВЗ серии микросхем К555 (ТТЛШ). Шифратор имеет 9 инверсных входов, обозначенных через PR1,..., РР9. Аббревиатура PR обозначает «приоритет». Шифратор имеет четыре ин­версных выхода В\,..., В8. Аббревиатура В означает «шина» (от англ. bus). Цифры определяют значение актив­ного уровня (нуля) в соответствующем разряде двоично­го числа. Например, В8 обозначает, что ноль на этом вы­ходе соответствует числу 8. Очевидно, что это неполный шифратор.

Если на всех входах — логическая единица, то на всех выходах также логическая единица, что соответствует чис­лу 0 в так называемом инверсном коде (1111). Если хотя бы на одном входе имеется логический ноль, то состоя­ние выходных сигналов определяется наибольшим номе­ром входа, на котором имеется логический ноль, и не за­висит от сигналов на входах, имеющих меньший номер.

Например, если на входе PR\ — логический ноль, а на всех остальных входах — логическая единица, то на выходах име-ются следующие сигналы: В1 - О, В2 -1, В4 -1, В8 -1, что соответствует числу 1 в инверсном коде (1110).

Если на входе PR9 логический ноль, то независимо от других входных сигналов на выходах имеются следующие

сигналы: В1 — 0, В2-1, В4-\,. 88-0, что соответствует числу 9 в инверсном коде (0110).

Основное назначение шифратора — преобразование номера источника сигнала в код (например, номера нажа­той кнопки некоторой клавиатуры).

Для получения шифраторов с большим числом входов, т. е. наращивания размерности шифратора, объединяют микросхемы шифраторов с дополнительными выводами.

Так микросхема К555ИВ1 (рис. 3.64) представляет со­бой приоритетный шифратор 8 х 3, т. е. имеет 8 инверсных входов и 3 инверсных выхода. Помимо этого она имеет вход разрешения EI, выход переноса Е0 и выход G, опре­деляющий признак входного информационного сигнала.

Если на всех информационных входах логическая 1, то при подаче на вход EI логического 0, на выходах 1—2—4 и G будут такие логические 1, а на выходе переноса ЕО — логический 0.

Если активизировать один из информационных входов (подать на него логический 0), то на выходах 1—2—4 появится инверсный код, соответствующий номеру активи­зированного входа, на входе G — логический 0, являю­щийся признаком подачи входного сигнала, а на выходе ЕО — логическая 1.

Если же микросхема не активизирована, т. е. на вход разрешения Е1 подана логическая 1, то на всех выходах микросхемы также будет логическая 1 независимо от того, что будет подано на информационные входы.

Дешифратором называется комбинационное устрой­ство, преобразующее n-разрядный двоичный код в логи­ческий сигнал, появляющийся на том выходе, десятичный номер которого соответствует двоичному коду. Число вхо­дов и выходов в так называемом полном дешифраторе свя­зано соотношением

т = , где п — число входов, а т — число выходов. Если в работе дешифратора используется неполное число выходов, то такой дешифратор называет­ся неполным. Так, например, дешифратор, имеющий 4 входа и 16 выходов, будет полным, а если бы выходов было только 10, то он являлся бы неполным.

Обратимся для примера к дешифратору К555ИД6 се­рии К555 (рис. 3.65). Дешифратор имеет 4 прямых входа, обозначенных через А\,..., Л8. Аббревиатура А обознача­ет «адрес» (от англ. address). Указанные входы называют адресными. Цифры определяют значения активного уров­ня (единицы) в соответствующем разряде двоичного числа.

Дешифратор имеет 10 инверсных выходов У0,..., К9. Цифры определяют десятичное число, соответствующее заданному двоичному числу на входах. Очевидно, что этот дешифратор неполный.

Значение активного уровня (нуля) имеет тот выход, номер которого равен десятичному числу, определяемому двоичным числом на входе. Например, если на всех вхо­дах — логические нули, то на выходе ко— логический ноль, а на остальных выходах — логическая единица. Если на входе А2 — логическая единица, а на остальных вхо­дах — логический ноль, то на выходе Y2 — логический ноль, а на остальных выходах — логическая единица. Если на входе — двоичное число, превышающее 9 (например, на всех входах единицы, что соответствует двоичному чис­лу 1111 и десятичному числу 15), то на всех выходах — ло­гическая единица.

Помимо информационных имеется один или более входов, называемых входами разрешения, или адресными входами. Так, микросхема КР531ИД14 представляет собой два дешифратора 2 х 4, т. е. каждый дешифратор имеет два информационных входа и четыре инверсных выхода, а также инверсный вход разрешения (рис. 3.66).

9.2 Сумматоры и полусумматоры.

Полусумматор это логическая цепь, которая вырабатывает сигналы суммы (S) и переноса (С) при сложении двух двоичных чисел а и в.

Составим таблицу функционирования.

Из таблицы получим:

. – сигнал суммы;

- сигнал переноса.

Эти выражения упрощению не поддаются.

Приведем к виду, удобному для реализации на элементах ИЛИ-НЕ.

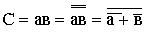
Исходя из полученных формул составим схему полусумматора (рис. 2.31, а):

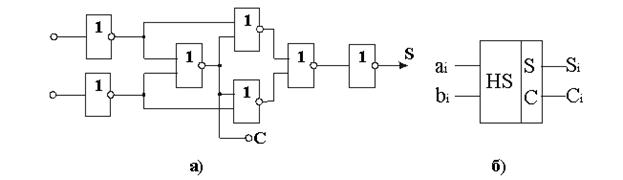
Рисунок 2.31 – Схема полусумматора

Поскольку полусумматор имеет широкое применение и его выпускают в виде отдельной микросхемы, он имеет собственное обозначение (рис. 2.31 б).

Составляя дизъюнктивную нормальную форму для полусумматора, мы получили следующие булевы функции:

Следовательно, перенос происходит с помощью функции И, а выработка сигнала суммы (функции неравнозначности) производится элементом ИСКЛЮЧАЮЩЕЕ – ИЛИ. На рис.2.32 показана схема полусумматора, составленная из этих элементов.

Рисунок 2.32 – Схема полусумматора.

Сумматор. В отличие от полусумматора должен воспринимать 3 входных сигнала: 2 слагаемых и сигнал переноса с предыдущего разряда.

Сумматором называется операционный узел ЭВМ, выполняющий операцию арифметического сложения двух чисел.

Чтобы понять сущность работы комбинационного сумматора, рассмотрим примеры суммирования двух одноразрядных двоичных чисел:

Из приведенных примеров (1 - 4) видно, что если отсутствует перенос из младшего разряда, то перенос в старший разряд может быть только в одном случае, когда оба числа равны единице. Если же имеется перенос из младшего разряда, то перенос в старший разряд будет всегда, кроме одного случая, когда оба слагаемых равны нулю.

Составим таблицу функционирования:

Таблица 15

Схема сумматора может быть реализована на двух полусумматорах, соединенных как указано на схеме рис. 2.33. В этой схеме выделим промежуточные сигналы P_i, g_i, r_i. Введем эти сигналы в новую таблицу функционирования. Соответствие работы этой схемы (рис. 2.33) и таблицы фунционирования можно проверить перебором всех возможных вариантов.

Рисунок 2.33 – Схема полного сумматора

Многоразрядный сумматор с последовательным переносом. Таким образом, в общем случае для каждого разряда необходима логическая схема с тремя входами a_i, b_i, C_i и двумя выходами S_i, C_i+1. Такая схема и есть полный сумматор. Ее можно реализовать с помощью двух полусумматоров.

Таблица 16

Для сложения двух многоразрядных двоичных чисел на каждый разряд необходим один полный сумматор. Только в младшем разряде можно обойтись полусумматором. На рис. 2.34 приведена схема, предназначенная для сложения двух четырехразрядных чисел А и В. Эта схема выпускается в интегральном исполнении. В ее младшем разряде также используется полный сумматор, чтобы иметь возможность наращивания разрядности схемы.

Рисунок 2.34 – Сумматор с последовательным переносом

Сумматоры с параллельным переносом. Время выполнения операции в сумматоре с параллельным переносом намного больше времени сложения в одноразрядном сумматоре. Действительно, сигнал переноса С₄ только тогда может принять истинное значение, когда будет установлено правильное значение С₃. Такой порядок выполнения операций называется последовательным переносом (Ripple Carry).

Чтобы уменьшить время операции сложения многоразрядных чисел можно использовать схемы параллельного переноса (Carry look-ahead). При этом все сигналы переноса вычисляются непосредственно по значениям входных переменных.

Согласно таблице переключений, в общем случае для сигнала переноса любого i-го разряда справедливо соотношение:

(1)

Величины g_i, r_i вычисляются в качестве промежуточных результатов и в полном сумматоре. Следовательно, их получение не требует дополнительных затрат. Смысл этих величин объясняется совсем просто. Сигнал g_i вырабатывается тогда, когда в данном разряде перенос происходит из-за комбинации входных переменных a_i,b_i. Поэтому его называют функцией генерации переноса. Сигнал P_i показывает, передается ли полученный в младшем разряде сигнал переноса C_i дальше. Поэтому он называется функцией распространения переноса.

Пользуясь выражением (1), можно вывести следующие формулы для вычисления сигналов переноса:

(2)

Очевидно, что хотя полученные выражения достаточно сложные, время формирования сигнала переноса в любой разрад с помощью вспомогательных функций определяется только времением здержки распространения сигнала на двух элементах. Эти функции реализуются специальным комбинационным устройством – схемой ускоренного переноса.

Схема сумматора с параллельным переносом приведена на рис. 2.35, а. На рис. 2.35, б изображена схема устройства параллельного переноса в группе из четырех разрядов. Эта схема реализует систему уравнений (2).

Рисунок 2.35 –Схема сумматора с параллельным переносом

Рисунок 2.36 –Схема ускоренного переноса

Схема выпускается в интегральном исполнении.

Сложение чисел, содержащих более четырех разрядов, можно реализовать подключением нескольких четырехразярадных сумматоров.

Дата добавления: 2014-01-07