Множительно-суммирующие блоки

Множительно-суммирующий блок для четырехразрядных операндов без набо­ра конъюнкторов, вырабатывающих члены вида а_ib_j, показан на рис. 2.37, а, где для одноразрядного сумматора принято обозначение (рис. 2.37, б).

Для построения МСБ чисел равной разрядности потребовалось n² конъюнк­торов и n² одноразрядных сумматоров.

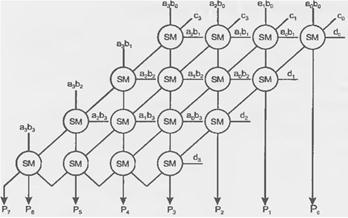
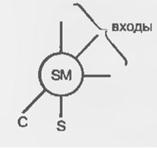
Рис. 2.37. Схема множительно-суммирующего блока для четырехрезрядных сомножителей (а), обозначение одноразрядного сумматоре для данной схемы (б)

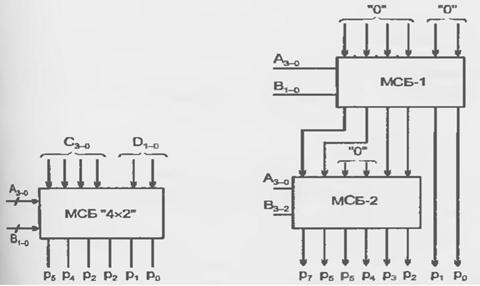
Рис. 2.38. К пояснению принципа наращивания размерности множительных устройств (в), условное обозначение множительно-суммирующего блока (б) и схема умножителя 4x4", построенная на множительно-суммирующих блоках "4 х 2" (в)

Максимальная длительность умножения — сумма задержек сигналов в конъюнкторах для выработки членов а_ib_j и задержки в наиболее длинной цепочке передачи сигнала в матрице одноразрядных сумматоров, равной 2n - 1 (m + n - 1 в общем случае). Таким образом, t_МРL = t_к + (2n - 1)tsм,

Схема множительного блока отличается от схемы МСБ тем, что в ней отсут­ствуют сумматоры правой диагонали, т. к. при С_m = 0 и D _n = 0 они не тре­буются.

Построение умножителей большей размерности из умножителей меньшей размерности на основе МБ требует введения дополнительных схем, называе­мых "деревьями Уоллеса", которые имеются в некоторых зарубежных сериях. При использовании МСБ дополнительные схемы не требуются. Принцип на­ращивания размерности умножителя иллюстрируется на рис. 2.38, а на примере построения МРЬ "4 х 4" из МСБ "4 х 2". На поле частичных произве­дений выделены зоны, воспроизведение которых возможно на блоках раз­мерности 4x2 (это две первые строки и две последние).

Перемножение в пределах зон дает частичные произведения р1 = Р51Р41РЗ1Р21Р11Р01 и Р2 = Р52Р42Р32Р22Р12Р02. Для получения конечного значения произведения эти частичные произведения нужно сложить с учетом их взаимного положения (сдвига одного относительно другого).

Схема, реализующая указанный принцип, изображена на рис. 2.38, в. В ней использовано условное обозначение МСБ (рис. 2.38, б). Для общности оба блока размерности 4x2 показаны как МСБ, хотя первый может быть про­сто множительным блоком, т. к. для него слагаемые С и D имеют нулевое значение.

Дата добавления: 2014-01-07