
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследование уравнений Эйлера
В правую часть дифференциальных уравнений Эйлера для движущейся идеальной жидкости входит величина dux. Её можно представить как полный дифференциал функции независимых переменных для dux, который можно записать в виде:
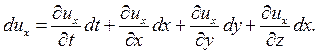
Тогда это уравнение для dux после деления на dt будет выглядеть:
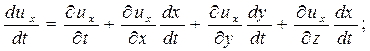
где: 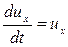 - проекция скорости u на ось X.
- проекция скорости u на ось X.
Тогда окончательно получим:
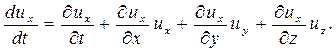
По аналогии то же самое можно записать и для других осей. С учётом таких преобразований система дифференциальных уравнений Эйлера для движущейся жидкости примет вид:
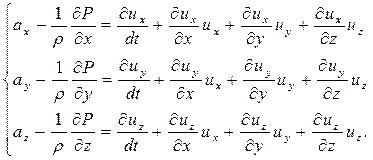
Физический смысл частных производных в уравнениях Эйлера рассмотрим на примере изменения скорости только по одной координате X.
 Слагаемое
Слагаемое 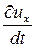 описывает изменение скорости жидкости во времени, т.е. характеризует неустановившийся режим течения жидкости. Если течение установившееся, то это слагаемое равно нулю.
описывает изменение скорости жидкости во времени, т.е. характеризует неустановившийся режим течения жидкости. Если течение установившееся, то это слагаемое равно нулю.
Величины  - прямые частные производные. Они описывают изменение скорости вдоль оси в зависимости от той же координаты.
- прямые частные производные. Они описывают изменение скорости вдоль оси в зависимости от той же координаты.
 Члены
Члены 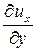 и
и  - косые частные производные, т.е. производные по смежной координате, показывающие, как изменяется значение скорости в направлении x (в проекции на ось X) в зависимости от изменения координат на перпендикулярных осях Y и Z. Рассмотрим их подробнее. В момент времени t1 скорость жидкости в точке A
- косые частные производные, т.е. производные по смежной координате, показывающие, как изменяется значение скорости в направлении x (в проекции на ось X) в зависимости от изменения координат на перпендикулярных осях Y и Z. Рассмотрим их подробнее. В момент времени t1 скорость жидкости в точке A 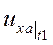 равна
равна  , а в точке B-
, а в точке B- 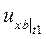 =
=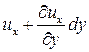 . Естественно, что приращение скорости по оси Y в этом случае составит
. Естественно, что приращение скорости по оси Y в этом случае составит 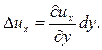
В момент времени t2 через бесконечно малый промежуток времени dt скорость в точке A 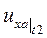 станет
станет 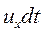 , а в точке B -
, а в точке B - 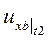 =
= 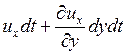 . Тогда тангенс угла dα можно вычислить по формуле:
. Тогда тангенс угла dα можно вычислить по формуле:
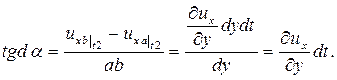
Учитывая, что при малых углах их тангенсы равны самим углам, можно записать 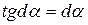 . Тогда
. Тогда 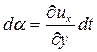 . Переписав последнее выражение, окончательно получим:
. Переписав последнее выражение, окончательно получим:
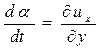 .
.
Это соотношение показывает, что рассмотренная частная производная есть ни что иное, как угловая скорость вращения бесконечно малого отрезка ab относительно оси Y (т.е., это соотношение описывает вращение вокруг «третьей» оси).
Таким же образом можно исследовать и остальные частные производные
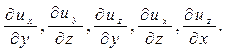
По аналогии с приведёнными выше рассуждениями можно утверждать, что частная производная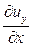 , так же как и
, так же как и 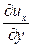 , описывает вращение частиц жидкости в плоскости XY относительно оси Z, частные производные
, описывает вращение частиц жидкости в плоскости XY относительно оси Z, частные производные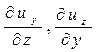 описывают вращение частиц жидкости в плоскости YZ относительно оси X, а частные производные
описывают вращение частиц жидкости в плоскости YZ относительно оси X, а частные производные 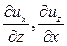 описывают вращение частиц жидкости в плоскости XZ относительно оси Y.
описывают вращение частиц жидкости в плоскости XZ относительно оси Y.
В заключение можно отметить, что такое движение можно наблюдать, например, в водоворотах, которые часто возникают вблизи сливных отверстий при сливе воды из ванн или раковин или в других похожих условиях.
|
|
Дата добавления: 2014-01-07; Просмотров: 413; Нарушение авторских прав?; Мы поможем в написании вашей работы!