Ламинарное течение жидкости

Напомним, что ламинарное течение - это упорядоченное слоистое течение, математическое описание которого основано на законе трения Ньютона.

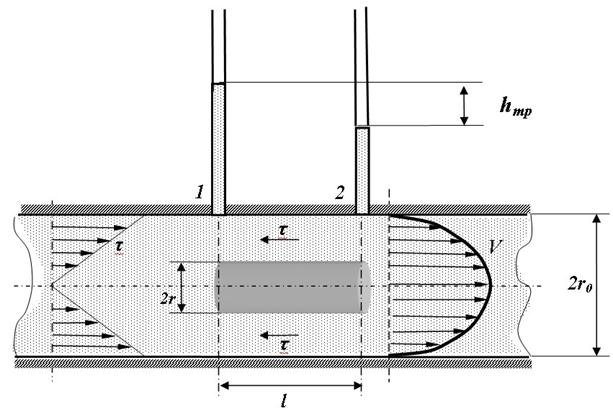
Для начала рассмотрим установившееся ламинарное течение в круглых трубах. В трубе диаметром 2r₀ выделим цилиндрический объём жидкости между сечениями 1 и 2 длиной l и диаметром 2r. Отметим, что давления в сечениях 1 и 2 соответственно равны P₁ и P₂. Распределение скоростей по сечению потока на всей длине трубы одинаково, поэтому одинаково и значение коэффициента кинетической энергии α. На рассматриваемый объём, движущийся со скоростью V, действуют силы давления (на торцовые поверхности) и силы сопротивления, вызванные вязким трением τ на боковой поверхности. Как уже было получено выше

,

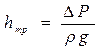а уравнение сил, действующих на выделенный объём, будет выглядеть

.

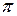
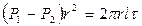Выразив отсюда 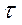, получим

.

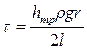Из последней формулы следует, что касательные напряжения трения линейно зависят от радиуса потока. Это показано на рисунке. С другой стороны, касательные напряжения по закону Ньютона равны

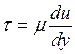или, в нашем случае 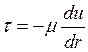т.к. разница скоростей между соседними потоками жидкости зависит от радиуса r. Знак «-» в формуле означает, что отсчёт по r направлен от оси к стенке, а при отсчете по y - от стенки к оси потока. Тогда

.

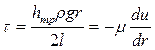Из этого соотношения можно найти приращение скорости

,

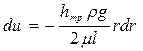т.е. при увеличении радиуса скорость уменьшается, что соответствует эпюре скоростей.

После интегрирования, получим

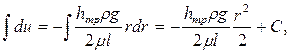
Постоянную интегрирования C легко определить из известных условий у стенки трубы, т.е. при r = r₀, u = 0. С учётом этих условий C примет вид 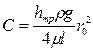. И тогда скорость в ламинарном потоке в зависимости от радиуса (а практически это скорость цилиндрического слоя жидкости, состоящего из элементарных струек, расположенных на одном радиусе в цилиндрическом потоке) будет описываться формулой

,

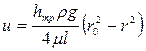которая, с математической точки зрения, является квадратной параболой и очерчивает эпюру распределения скоростей по сечению потока. Максимальное значение скорости достигается в центре потока при r=0 и составляет

.

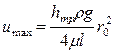Используя значение скорости u, определим величину расхода через кольцевую площадь dω_c шириной dr, находящуюся на расстоянии r от центра трубы. Выше было отмечено, что скорость в любой точке этого кольца одинакова, и тогда

.

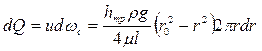Проинтегрировав dQ по всей площади трубы (т.е. от r = 0 до r = r₀), получим

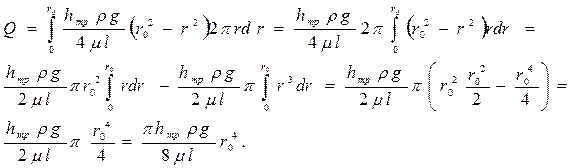
Средняя скорость в таком потоке будет

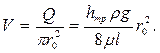
Заметим, что средняя скорость потока с параболическим распределением скоростей вдвое меньше максимальной.

Из последнего выражения легко получить закон сопротивления потоку, т.е. зависимость потерь энергии от размеров и параметров движения жидкости:

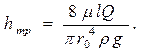
Заменив в этом выражении динамический коэффициент вязкости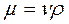кинематическим и выразив радиус трубы r₀ через диаметр d, получим

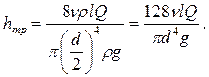
Полученное выражение носит название закона Пуазейля и применяется для расчета потерь энергии с ламинарным течением.

Эту же величину потерь на трение ранее мы выразили формулой Дарси. Если приравнять правые части формулы Дарси и закона Пуазейля, получится:

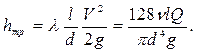
Заменим расход произведением 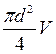и подставим в последнее равенство

.

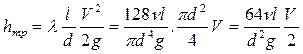Искусственно умножим и разделим числитель и знаменатель на V:

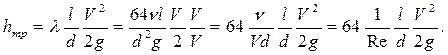
Очевидно, что в этом случае

.

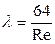Это выражение для коэффициента гидравлического трения при ламинарном движении жидкости хорошо подтверждается экспериментом и используется на практике для определения потерь энергии в потоке при ламинарном течении. Иногда этот коэффициент обозначается .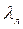

Зная полученные выше выражения для скорости элементарной струйки u и для средней скорости потока V, можно вычислить значение коэффициента кинетической энергии 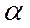в уравнении Бернулли, который является отношением действительной кинетической энергии к кинетической энергии, посчитанной с применением средней скорости

.

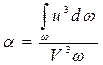Учтём, что 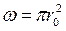, , 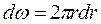скорост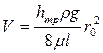и и 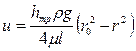. Переменную интегрирования ω (площадь живого сечения) заменим радиусом. После подстановки в выражение для α получим:

.

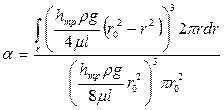Раскроем интеграл в числителе

.

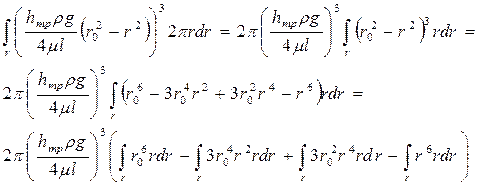Проинтегрируем эту функцию в пределах от 0 до r₀, т.е. по сечению потока

.

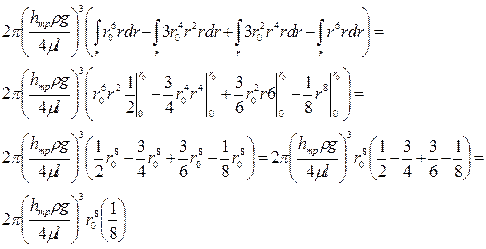Теперь рассмотрим знаменатель выражения для α:

.

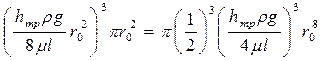Разделив полученные числитель на знаменатель, будем иметь значение коэффициента кинетической энергии α:

.

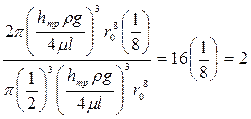Это значит, что кинетическая энергия ламинарного потока с параболическим распределением скоростей вдвое превышает кинетическую энергию того же потока с равномерным распределением скоростей.

В некоторых случаях удобно знать другой поправочный коэффициент, который учитывает отличие действительного количества движения потока от его значения, посчитанного с использованием средней скорости потока V. Этот коэффициент обозначают α₀, называют коэффициентом количества движения и вычисляют по формуле

.

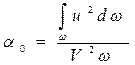По аналогии с вычислением коэффициента α, подставив вместо u и V соответствующие выражения, после возведения в квадрат и замены переменной интегрирования получим для числителя:

.

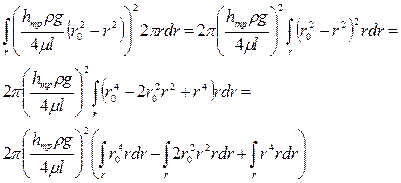После интегрирования в пределах от 0 до r₀, числитель примет вид

.

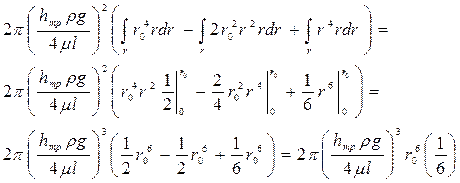Знаменатель выражения для α перепишем в виде

.

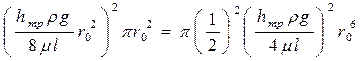После деления числителя на знаменатель получим значение коэффициента количества движения α₀:

.

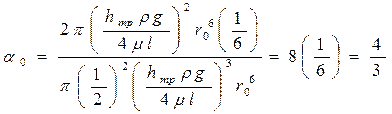Эта величина для ламинарного потока с параболическим распределением скоростей, так же как и α, является величиной постоянной.

Все приведённые зависимости справедливы для участков прямых гладких труб постоянного сечения с параболическим распределением скоростей по живому сечению потока.

Дата добавления: 2014-01-07