Внезапное расширение. Теорема Борда - Карно

Виды местных сопротивлений

В этом случае, одном из немногих, выражение для потери напора можно найти теоретическим путем.

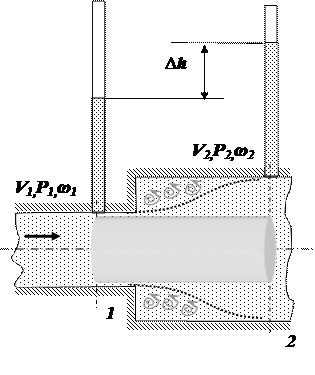При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот. На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Тогда появляется вопрос, о каких потерях идёт речь? Дело в том, что показания пьезометра зависят не только от потерь энергии, но и от величины давления. А давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае надо учитывать, что если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше.

Происходящая при внезапном расширении потеря напора может быть найдена с помощью уравнения Бернулли для потока реальной жидкости, записанного для сечений 1 и 2, где движение основного потока занимает всё сечение трубы, которое будет иметь вид:

.

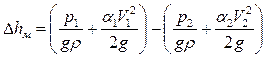Применим теорему механики об изменении количества движения к выделенному цилиндрическому объёму, заключённому между сечениями 1 и 2, равному импульсу внешних сил, действующих на рассматриваемый объём в направлении его движения. Этими силами будут силы от давления 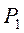и 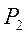в соответствующих сечениях, действующие на равные по размеру торцовые площади 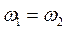. (Изменением давления по высоте потока в трубе и силами трения из-за малости участка пренебрежём.) Разность этих сил составляет величину

.

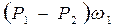Этому импульсу соответствует секундное изменение количества движения жидкости, втекающей в рассматриваемый объём и вытекающей из него. Если считать, что скорости по сечениям распределены равномерно, получим:

.

Приравняем импульс сил и изменение количества движения по теореме об изменении количества движения

.

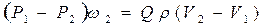Разделим уравнение на 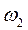и учтём, что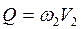

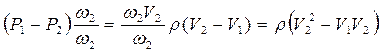
Далее произведём сокращения, заменив величину 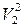суммой 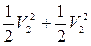. Искусственно добавим в правую часть и тут же вычтем величину :

.

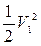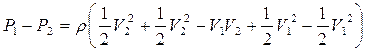Перегруппируем члены в правой части равенства

.

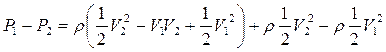Заметим, что величина в скобках может быть упрощена

.

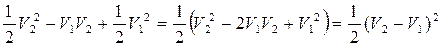Проведя замену, получим

.

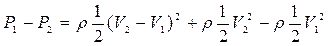После перегруппировки членов получим

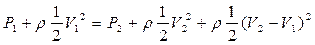
Разделим все члены равенства на

.

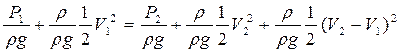Окончательно уравнение примет вид

.

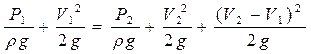Сравним полученное уравнение с исходным уравнением для 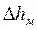, полученным из уравнения Бернулли: .

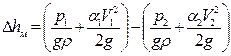Если допустить, что форма эпюр скоростей в первом и втором сечении одинакова, т.е. 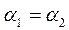и их значения приближаются к единице т.к. поток турбулентный, и поменять местам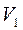и и 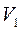, т.к. 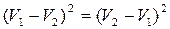, то из сравнения последних уравнений можно получить, что:

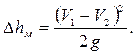
Назвав разность 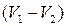потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.

Последнюю формулу можно переписать в виде:

или .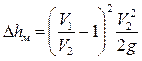

С учетом того, что на основании уравнения неразрывности потока 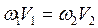, те же потери напора можно представить в виде:

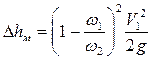или .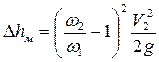

Сравнивая последние выражения с формулой Вейсбаха 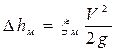, можно выделить выражения для коэффициента местного сопротивления при внезапном расширении потока:

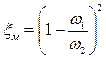, если 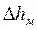определять по скорости ;

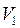, если 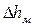определять по скорости .

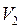Дата добавления: 2014-01-07