
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упрощение формул
|
|
|
|
Введем некоторые соглашения о записи и вычислениях формул.
1) В формулах будем опускать внешнюю пару скобок, т.е. вместо формулы (х ® у) будем писать выражение х ® у. Аналогично в выражениях со знаком отрицания вместо 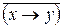 будем записывать
будем записывать 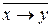 .
.
2) По закону ассоциативности для операции «∘» вместо формулы ((x ∘ y) ∘ z) или (x ∘(y ∘ z)) можно использовать выражение без скобок: x ∘ y ∘ z. Для восстановления формулы достаточно расставить скобки, порядок которых не является существенным для вычислений.
3) Введем также соглашения о старшинстве операций: если в выражении с помощью скобок специально не указан порядок выполнения операций, то одинаковые по старшинству операции выполняются последовательно слева направо. Если в выражении имеются различные операции, то сначала выполняется отрицание, затем конъюнкция, дизъюнкция, импликация и т.д., самой последней выполняется эквиваленция. Скобки восстанавливаются по тому же правилу, например, в выражении х ÚØ у ® z º t скобки восстанавливаются в следующем порядке:
х Ú(Ø у)® z º t
(х Ú(Ø у))® z º t
((х Ú(Ø у))® z)º t
(((х Ú(Ø у))® z)º t)
Ввиду введенного старшинства операций не всякая формула может быть записана без скобок. Например, в выражениях х ®(у ® z) или х &(y Ú z) дальнейшее исключение скобок невозможно, т.к. это может повлиять на значение, вычисленное по формуле.
4) В дальнейшем для компактности будем использовать следующую запись 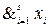 вместо х 1& x 2&…& xs, а также
вместо х 1& x 2&…& xs, а также  вместо х 1Ú x 2Ú…Ú xs.
вместо х 1Ú x 2Ú…Ú xs.
Из свойств элементарных функций следует ряд простых правил преобразования формул:
а) если один из сомножителей логического произведения равен нулю, то значение произведения также равно нулю;
б) если логическое произведение содержит не менее двух сомножителей, один из которых равен единице, то этот сомножитель можно сократить;
в) если логическая сумма содержит не менее двух слагаемых, одно из которых принимает значение ноль, то его можно сократить;
г) если хотя бы одно из слагаемых логической суммы принимает значение единица, то и вся логическая сумма равна единице;
д) пусть U1 – подформула формулы U; если в формуле U заменить любые вхождения подформулы U1 эквивалентной ей формулой В1, то в результате будет получена формула В, эквивалентная исходной формуле U.
Перечисленные свойства и правила позволяют преобразовывать формулы, получая новые тождества.
Рассмотрим эквивалентные преобразования формулы:  1=
1= 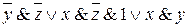 2=
2= 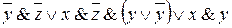 3=
3= 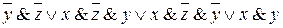 4=
4= 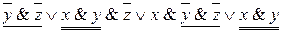 5=
5= 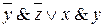
Тождество 1 записано по правилу сокращения единичного сомножителя, тождество 2 – по правилу замены подформулы эквивалентной формулой, а именно: здесь для замены использовался закон исключенного третьего. В тождестве 3 применяется закон дистрибутивности. Тождество 4 получено по закону коммутативности. И, наконец, тождество 5 записано по закону поглощения, причем для наглядности «поглощающие элементы» подчеркнуты одинарной и двойной чертой.
Помимо описанных правил эквивалентных преобразований формул имеются также другие способы получения новых тождеств, которые основаны на понятии двойственности.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 455; Нарушение авторских прав?; Мы поможем в написании вашей работы!