Тупиковые ДНФ и алгоритм наискорейшего спуска

Этот метод основан на двух преобразованиях, упрощающих ДНФ: удаление конъюнкции и удаление множителя.

Первое преобразование возможно тогда, когда исходная ДНФ и ДНФ, получающаяся после удаления некоторой элементарной конъюнкции, совпадают на всех наборах значений переменных { x ₁, x ₂, …, x_n }.

Аналогично второе преобразование возможно в тех случаях, когда получающаяся после удаления множителя из некоторой элементарной конъюнкции ДНФ, продолжает реализовывать исходную функцию.

ДНФ, которую нельзя упростить с помощью этих двух преобразований, называют тупиковой ДНФ (ТДНФ) относительно удаления конъюнкции и множителей в конъюнкциях. Например, ДНФ=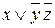является тупиковой.

Важно, что указанные преобразования уменьшают сложность ДНФ, одна и та же функция может иметь несколько различных тупиковых ДНФ, среди которых всегда содержатся и минимальные, хотя не обязательно все.

Опишем алгоритм по шагам.

Шаг 1. Для функции f (x ₁, x ₂, …, x_n), заданной таблицей, записывается СДНФ, которая считается исходной ДНФ.

Шаг 2. Исходная ДНФ просматривается слева направо. Для текущей конъюнкции исходной ДНФ пытаются применить первое преобразование – удаление конъюнкции. Если это преобразование возможно, то переходят к следующей конъюнкции и т.д.. В противном случае переходят к шагу 3.

Шаг 3. Поочередно (слева направо) рассматривают каждый множитель текущей элементарной конъюнкции с целью применения преобразования «удаление множителя». После просмотра всех множителей этой конъюнкции текущей становится следующая конъюнкция, и процесс возвращается к шагу 2.

После того, как будут рассмотрены все элементарные конъюнкции исходной ДНФ, приступают к выполнению шага 4.

Шаг 4. Полученную в результате выполнения предыдущих шагов ДНФ снова исследуют слева направо, поочередно рассматривая каждую элементарную конъюнкцию. Однако на этот раз пытаются применить только первое преобразование, не переходя ко второму.

ДНФ, полученная в итоге, является тупиковой относительно введенных преобразований.

Для получения других ТДНФ той же функции в исходной СДНФ переупорядочивают множители в элементарных конъюнкциях. Число таких переупорядочиваний в общем случае не превышает (n!) ^s, где s – число элементарных конъюнкций в исходной СДНФ, а n – число переменных функции. Но s £2 ⁿ, поэтому (n!) ^s £(n!)^{2 n}. Для каждой СДНФ необходимо выполнить не менее s операций по проверке удаления конъюнкций на втором шаге и не более s таких же операций на четвертом шаге. Кроме того, в каждой конъюнкции возможно выполнение n операций по проверке удаления множителя на третьем шаге. Так что общее число проверок для одной СДНФ не больше, чем s + s + n · s = s ·(n +2) £ 2 ⁿ ·(n +2). Тем самым трудоемкость построения минимальных ДНФ по этому алгоритму не превышает (n!)^{2 n} ·(n +2)·2 ⁿ, что меньше, чем 2^{3 n}. Таким образом, трудоемкость метода «наискорейшего спуска» меньше трудоемкости тривиального алгоритма, но для «ручного» просчета слишком велика. Однако алгоритм легко программируется для решения задачи на компьютере.

Таблица 21

x	y	z	f (x, y, z)

Пример:

Пусть функция трех переменных f (x, y, z) задана таблицей 21. Запишем СДНФ этой функции: СДНФ(f) =

Оформим все вычисления в виде таблицы 22.

Таблица 22

ДНФ	Текущая конъюнкция	Текущий множитель	Примечание
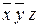
1.			не удаляется
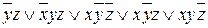
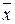
2.			удаляется
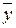
			не удаляется
		z	не удаляется
			не удаляется
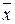
			не удаляется
3.		y	удаляется
		z	не удаляется
			не удаляется
		x	не удаляется
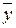
4.			удаляется
			не удаляется
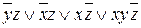
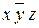
5.			удаляется
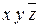
6.			удаляется
			не удаляется
			не удаляется
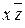
			не удаляется

Таким образом, ТДНФ₁(f) =

Теперь переставим в третьей конъюнкции исходной ДНФ множитель вперед, тогда новый ход вычислений представится таблицей 23:

Таблица 23

ДНФ	Текущая конъюнкция	Текущий множитель	Примечание
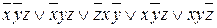
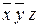
1.			не удаляется
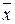
2.			удаляется
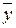
			не удаляется
		z	не удаляется
			не удаляется
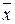
			не удаляется
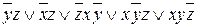
3.		y	удаляется
		z	не удаляется
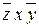
			не удаляется
4.			удаляется
		x	не удаляется
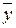
			не удаляется
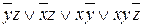
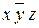
5.			удаляется
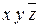
			не удаляется
		x	не удаляется
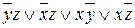
6.		y	удаляется
			не удаляется
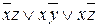
7.			удаляется
			не удаляется
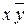
			не удаляется
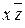
			не удаляется

Таким образом, ТДНФ₂(f) =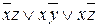

В данном примере другие перестановки множителей в конъюнкциях СДНФ уже не приведут к новым результатам. Кроме того, обе найденные тупиковые ДНФ являются также и минимальными для этой функции.

Дата добавления: 2014-01-07