Аналитическое построение сокращенной ДНФ

Сокращенная ДНФ обладает тем свойством, что записывается единственным образом для каждой булевой функции. Кроме того, любая ТДНФ, а следовательно и любая МДНФ, получается из сокращенной ДНФ (СокрДНФ) путем удаления из нее некоторых элементарных конъюнкций.

Для построения СокрДНФ обычно используется задание функции в виде СДНФ или произвольной ДНФ. Наиболее универсальным методом перехода к СокрДНФ является выполнение над исходной ДНФ преобразований вида:

а) A Ú AB = A – поглощение, где A и B – элементарные конъюнкции;

б) x A Ú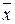 B = x A Ú 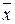B Ú AB – склеивание;

или x A Ú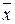 A = A – полное склеивание;

или x A Ú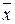 A = x A Ú 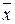A Ú A – неполное склеивание.

При этом вначале следует выполнить всевозможные попарные склеивания входящих в ДНФ элементарных конъюнкций, а затем поглощения. Далее, если это возможно, преобразования применяют повторно. При этом сложность полученной СокрДНФ может оказаться больше сложности исходной ДНФ.

Примеры:

1) Пусть функция трех переменных f (x, y, z) задана в виде СДНФ:

f (x, y, z) =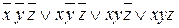

Выполним всевозможные попарные склеивания, т.е. будем склеивать первую конъюнкцию со второй, третьей, четвертой, затем вторую с третьей и четвертой, и наконец, третью с четвертой.

Тогда f (x, y, z) =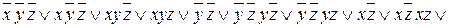

Ú x y =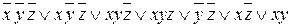

Теперь выполняя всевозможные поглощения, получим:

f (x, y, z) = .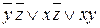

Последняя формула является СокрДНФ.

2) Теперь рассмотрим функцию трех переменных f (x, y, z), заданную формулой вида ДНФ: f (x, y, z) =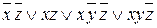

При склеивании первой и второй конъюнкции получим 0, склеивание всех остальных пар добавит к исходной ДНФ дополнительные конъюнкции и тогда: f (x, y, z) = .

Выполняя поглощение, получим: f (x, y, z) =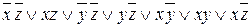

Теперь, применяя ещё раз склеивание и поглощение, переходим к следующей формуле:

f (x, y, z) = x Ú. И, поскольку преобразования больше невозможны, последняя формула является СокрДНФ.

Дата добавления: 2014-01-07