Диаграммы Вейча–Карно

Диаграмма Вейча - Карно представляет собой плоскую карту, на которой положение каждой ячейки определяется системой горизонтальных и вертикальных координат. Система координат вводится таким образом, чтобы при переходе от любой ячейки карты к любой другой, соседней с ней слева или справа, сверху или снизу ячейке, происходила бы смена только одной какой-нибудь координаты.

В каждую ячейку такой карты записывается значение функции на наборе, соответствующем координатам ячейки. Такие карты могут использоваться для представления функций, число переменных у которых не более 8. Очевидно, что для каждой булевой функции карта Карно заполняется единственным образом. И по заполненной карте Карно функция восстанавливается также однозначно. Структура и разметка карты для функций двух, трёх и четырёх переменных показана на рисунке 8.

			y z
x		f (0,0,0)	f (0,0,1)	f (0,1,1)	f (0,1,0)
	f (1,0,0)	f (1,0,1)	f (1,1,1)	f (1,1,0)

		y
x		f (0,0)	f (0,1)
	f (1,0)	f (1,1)

			z w
		f (0,0,0,0)	f (0,0,0,1)	f (0,0,1,1)	f (0,0,1,0)
x		f (0,1,0,0)	f (0,1,0,1)	f (0,1,1,1)	f (0,1,1,0)
y		f (1,1,0,0)	f (1,1,0,1)	f (1,1,1,1)	f (1,1,1,0)
		f (1,0,0,0)	f (1,0,0,1)	f (1,0,1,1)	f (1,0,1,0)

Рис. 8

По карте легко строится СДНФ и СКНФ функции f (x ₁, x ₂,..., x_n): каждой ячейке с единицей соответствует элементарная конъюнкция ранга n – 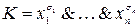, где s ₁,…, s_n – набор, отвечающий координатам ячейки, а каждой ячейке с нулем (пустой ячейке) соответствует элементарная дизъюнкция ранга n: .

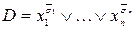Таблица 26

			y z
x

Для функции трех переменных, заданной картой Карно, приведенной в таблице 26, СДНФ =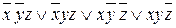

СКНФ =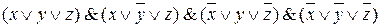

Ячейку карты можно рассматривать, как прямоугольную группу размера 2⁰´2⁰, и ранг соответствующей элементарной конъюнкции (дизъюнкции) r = n – 0 – 0.

Легко показать, что каждой прямоугольной группе соседних ячеек с единицами, размером 2 ^a ´2 ^b, соответствует элементарная конъюнкция (дизъюнкция) ранга (n ‑ a ‑ b). Для подтверждения этого рассмотрим карту функции в таблице 26. Две соседних ячейки с единицами в верхней строке таблицы образуют прямоугольную группу, размером 2⁰´2¹, поэтому соответствующая этой группе элементарная конъюнкция должна иметь ранг 3 – 1 – 0 = 2. Рассмотрим дизъюнкцию элементарных конъюнкций, соответствующих каждой из этих двух ячеек: 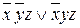. Выполним преобразования в этой формуле: 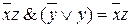. В результате преобразований получена конъюнкция 2‑го ранга. Теперь рассмотрим две соседних ячейки с нулями (пустые) в нижней строке той же таблицы. Конъюнкция двух элементарных дизъюнкций, соответствующих этим ячейкам: 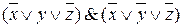после преобразований запишется в виде элементарной дизъюнкции 2‑го ранга: .

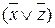Несложно сформулировать правило, позволяющее записать элементарную конъюнкцию (дизъюнкцию), соответствующую прямоугольной группе соседних ячеек с единицами (нулями), размером 2 ^a ´2 ^b. А именно: для записи элементарной конъюнкции надо воспользоваться разметкой координатных осей карты. Множители конъюнкции определяются неизменными координатами в данной группе ячеек, при этом множитель будет входить в конъюнкцию с отрицанием, если соответствующая ему координата равна нулю в этой группе ячеек, и без отрицания, если она равна единице. Для записи элементарной дизъюнкции также используются неизменные координаты рассматриваемой группы ячеек. Слагаемое будет входить в дизъюнкцию с отрицанием, если соответствующая ему координата равна единице, и без отрицания, если она равна нулю в этой группе ячеек.

Подтвердим сказанное примерами.

Таблица 27

			z w
		00
x
y

В таблице 27 приведена карта Карно функции четырех переменных. Вертикальной группе соседних ячеек с единицами (второй столбец таблицы), размером 2²´2⁰, соответствует элементарная конъюнкция 2‑го ранга K =.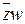

Группе ячеек с единицами в правом верхнем углу таблицы, размером 2¹´2¹, соответствует элементарная конъюнкция K =.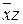

Группе из двух единиц слева в третьей строке таблицы, размером 2⁰´2¹, соответствует элементарная конъюнкция 3‑го ранга K = .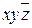

Двум пустым ячейкам в левом верхнем углу таблицы соответствует элементарная дизъюнкция 3‑го ранга: .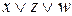

И, наконец, группе из четырех пустых ячеек в правом нижнем углу карты соответствует элементарная дизъюнкция 2‑го ранга: .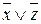

Таблица 28

			y z
x

С точки зрения формирования прямоугольных групп карты Карно для функций трех переменных рассматриваются как цилиндр, со склеенными правым и левым краями. Прямоугольные группы, формируемые на таком цилиндре, могут оказаться разорванными на плоском рисунке (см. таблицу 28). Однако правило для записи конъюнкции (дизъюнкции), соответствующей такой разорванной группе, остается прежним. Таким образом, для выделенных в таблице 28 единиц, образующих разорванную группу, соответствующая конъюнкция запишется в виде: .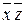

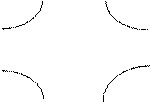
На картах с четырьмя переменными при формировании групп склеенными следует считать также верхний и нижний края. Таким образом, карта с четырьмя переменными рассматривается как поверхность тора. Прямоугольные группы, формируемые на торе, также могут оказаться разорванными на плоском рисунке. Но правило для записи элементарной конъюнкции (дизъюнкции) остается тем же.

Таблица 29 Таблица 30

			z w
y
x

			z w
y
x

Таким образом, для карты функции четырех переменных, представленной в таблице 29, соответствующая элементарная конъюнкция K =.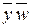

Для карты в таблице 30 конъюнкция, соответствующая группе из четырех единиц, K =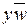и группе из двух единиц – K =.

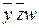Дата добавления: 2014-01-07