
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скольжение краевой дислокации
|
|
|
|
Давно установлено, что изменение формы кристалла при пластической деформации легко объяснить сдвиговым процессом. По аналогии со сдвигом карт в колоде или монет в стопке, когда направленное смещение каждой карты или монеты по отношению к соседней вызывает изменение формы и размеров всей колоды или стопки, происходит направленное скольжение одних тонких слоев кристалла по отношению к другим.
Это скольжение отчетливо проявляется на полированной поверхности кристалла в виде линий сдвига.
Сдвиги происходят по определённым кристаллографическим плоскостям, например, преимущественно по плоскостям {111} в кристаллах с гранецентрированной кубической решеткой и {0001} в кристаллах с гексагональной решеткой. Скольжение в определенной плоскости начинается тогда, когда касательное напряжение в ней достигает некоторой критической величины, называемой критическим скалывающим напряжением.
У монокристаллов большинства цветных металлов высокой чистоты при. комнатной температуре критическое скалывающее напряжение τкр~ 0,02-0,1 кгс/мм2.
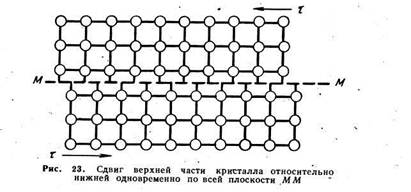
В додислокационной теории скольжение представлялось в виде одновременного смещения всех атомов одного слоя по отношению к атомам соседнего слоя (рис. 23), т. е. так, как скользят соседние карты в колоде. При этом приложенная сила должна быть достаточной, чтобы преодолеть взаимное притяжение между всеми граничными атомами из соседних слоев.
Оценим порядок величины критического скалывающего напряжения, соответствующего этой модели скольжения.
Рассмотрим две соседние атомные плоскости I и II (рис. 24) с межплоскостным расстоянием а. При смещении плоскости I относительно плоскости // в направлении, указанном стрелкой b, каждый атом смещающейся плоскости периодически, после продвижения на величину b, попадает в равновесные положения, неотличимые от исходных. В положениях равновесия (узлах решетки) энергия атомов минимальна, а при смещении плоскости I из положения равновесия на расстояние b /2 эта энергия достигает максимума.
Сила межатомного взаимодействия двух плоскостей вначале (при смещениях x< b /2 ) мешает удалению плоскости I от положения равновесия, а затем (при x> b /2 ) способствует принижению этой плоскости к новому положению равновесия. При x= b /2 сила, меняя знак, обращается в нуль: на полпути до нового положения равновесия атомы плоскости I с одинаковой силой притягиваются к соседним атомам слева и справа на плоскости II.
В первом приближении примем, что сила сдвига плоскости I соответствующее касательное напряжение изменяются в зависимости от смещения по синусоиде:

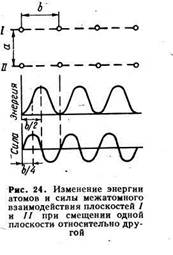 При x= b /4 сила сдвига проходит через максимум (см. рис. 24), соответствующий искомому критическому скалывающему напряжению. Постоянную k можно определить, рассматривая малые смещения, в области которых sin (2π x)/ b ~ - (2π x)/ b и зависимость касательного напряжения от смещений подчиняется закону Гука: τ = Gy, где относительный сдвиг
При x= b /4 сила сдвига проходит через максимум (см. рис. 24), соответствующий искомому критическому скалывающему напряжению. Постоянную k можно определить, рассматривая малые смещения, в области которых sin (2π x)/ b ~ - (2π x)/ b и зависимость касательного напряжения от смещений подчиняется закону Гука: τ = Gy, где относительный сдвиг
γ = x/a. Следовательно, в области малых смещений τ = k (2π x)/ b=G x/a. Отсюда k =(b/a)(G/2π). Подставляя это значение константы в выражение (10), получаем

Для определения критического скалывающего напряжения подставляем в формулу (11) значение x= b /4 и получаем
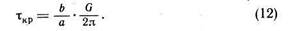
Межплоскостное расстояние а по порядку величины равно межатомному расстоянию в направлении сдвига b. Отсюда

Таким образом, при одновременном смещении всех атомов одного слоя по отношению к другому атомному слою необходимо приложить касательное напряжение, равное примерно G/6. Если принять более точный закон изменения межатомных сил в зависимости от смещения плоскостей, то величина τкр получится несколько меньшей, а именно ~ G/30. Так как модуль сдвига металлических монокристаллов имеет величину порядка 103 — 104 кгс/мм2, теоретическое значение критического скалывающего напряжения для пластической деформации с одновременным смещением всех атомов одного слоя относительно другого слоя должно быть равно 102—103 кгс/мм2, т. е. на 3—4 порядка выше экспериментально установленных значений.
 Следовательно, представление об одновременном смещении всех атомов одного слоя по отношению к атомам соседнего слоя кристалла противоречит очень низким опытным значениям критического скалывающего напряжения. Аналогия со сдвигом карт в колоде удовлетворительно объясняет лишь результат пластической деформации, а атомный механизм «сдвига» более сложен.
Следовательно, представление об одновременном смещении всех атомов одного слоя по отношению к атомам соседнего слоя кристалла противоречит очень низким опытным значениям критического скалывающего напряжения. Аналогия со сдвигом карт в колоде удовлетворительно объясняет лишь результат пластической деформации, а атомный механизм «сдвига» более сложен.
Чтобы объяснить низкое значение критического скалывающего напряжения, пришлось предположить, что при «сдвиге» соседних слоев межатомные силы преодолеваются не одновременно. В каждый момент времени в смещении участвуют не все атомы, находящиеся по обе стороны от плоскости скольжения, а лишь сравнительно небольшая группа атомов. Для описания такого механизма и было использовано представление об особом типе несовершенств в решетке — дислокациях. Рассмотрим схему атомного механизма перемещения краевой дислокации при сдвиге на одно межатомное расстояние (рис. 25)., В исходном состоянии положение атомов обозначено светлыми кружками, а в конечном — черными. Чтобы дислокация из исходного положения 1 переместилась в соседнее положение 14, не нужно сдвигать всю верхнюю половину кристалла на одно межатомное расстояние. Достаточно, чтобы произошли следующие перемещения атомов: атом 1 в положение 2, 3 в 4, 5 в 6, 7 в 8, 9 в 10, 11 в 12, 13 в 14, 15 в 16 и 17 в 18. Аналогичным образом смещаются атомы не только в плоскости чертежа, но и во всех атомных слоях, параллельных этой плоскости. Незначительные перемещения атомов в области несовершенства (дислокации) приводят к перемещению самой дислокации на одно межатомное расстояние. При этом целая плоскость 7 — 17 разрывается на две части. Ее нижняя часть объединяется с исходной экстраплоскостью в целую плоскость 8 — 6, а верхняя превращается в новую экстраплоскость 14 — 18.
Под действием касательных напряжений дислокация перемещается в плоскости скольжения ММ путем указанных выше перемещений атомов. Такое движение ее называется скольжением или консервативным движением.
На рис. 25 показаны краевая дислокация внутри кристалла и ступенька на его правой боковой грани, образовавшаяся в результате сдвига справа налево верхней части кристалла относительно нижней, причем зафиксирован момент, когда сдвиг еще не произошел в потенциальной плоскости скольжения левее дислокации. Если под действием сдвигающей силы дислокация будет скользить справа налево, то сдвиг будет охватывать все большую часть плоскости скольжения. Когда дислокация выйдет на левую боковую грань кристалла, здесь образуется ступенька.

На рис. 26 показаны разные положения дислокации при ее скольжении. Пунктиром отмечена часть кристаллографической плоскости, в которой уже произошел сдвиг на одно межатомное расстояние. Ступеньки величиной в одно межатомное расстояние на правой и левой гранях кристалла, образовавшиеся в результате пробега одной дислокации справа налево через весь кристалл, могли бы явиться следствием сдвига всей верхней части как единого целого по отношению к нижней части кристалла.
Однако в действительности сдвиг распространялся постепенно. В каждый момент времени в нем участвовали не все атомы по обе стороны от плоскости скольжения, а только те, которые находились в области дислокации, вокруг края экстраплоскости. Происходило поочередное, эстафетное перемещение атомов на расстояния меньше межатомного, в результате чего дислокация скользила на большие расстояния через весь кристалл. Если при одновременном сдвиге верхней части кристалла по отношению к нижней необходимо преодолеть межатомные связи между всеми граничными атомами по обе стороны от плоскости скольжения (см. рис. 23), то при перемещении дислокации в соседнее положение разрываются межатомные связи только между двумя цепочками атомов (между 11 и 13 на рис. 25). Именно этим объясняется низкое опытное значение критического скалывающего напряжения.
Развитие сдвига в кристалле при скольжении в нем краевой дислокации помогает также понять следующая аналогия (рис. 27). Ковер из положения AB можно переместить в положение A’В’ протаскивая его по полу как единое целое. Точно такой же конечный результат дает продвижение складки от одного края ковра до другого, но в этом случае в каждый момент времени требуется затрачивать меньшее усилие, чем при протаскивании по полу целиком всего ковра. Интересно, что змеи обычно ползают за счет образования складки («положительной дислокации») около хвоста и продвижения этой складки в сторону головы.

На рис. 26 показан сдвиг на одно межатомное расстояние при пробеге положительной краевой дислокации справа налево. Аналогичный результат получается при пробеге отрицательной краевой дислокации слева направо. Чтобы убедиться в этом, достаточно перевернуть рис. 26, превратив положительную дислокацию в отрицательную. Под действием одних и тех же сдвигающих напряжений дислокации разного знака движутся в прямо противоположных направлениях. Это также видно при переворачивании рис. 26. Скольжение дислокации не обусловлено диффузионными перемещениями атомов и может происходить при каких угодно низких температурах.
Заметим, что скольжение всегда происходит по плоскости, в которой находится и линия дислокации, и вектор сдвига.
Под легкостью скольжения дислокаций не следует понимать обязательную быстроту их движения. При низких приложенных напряжениях дислокации скользят очень медленно со скоростями порядка 10-7 см/с и менее.
Скорость скольжения дислокаций изменяется в очень широком диапазоне в зависимости от приложенного напряжения, температуры и других факторов. Теория этого вопроса разработана слабо. Эмпирически найдена следующая зависимость скорости скольжения дислокации v от приложенного касательного напряжения τ:

где τ0 — касательное напряжение, при котором скорость скольжения дислокации v0 = 1 см/с; т — константа материала.
Эта формула получена при исследовании разных по природе кристаллических веществ, но она не универсальна; имеются и другие эмпирические формулы, связывающие v с τ.
У разных материалов скорость скольжения дислокаций неодинаково возрастает с повышением приложенного напряжения, т.е. различен показатель т в формуле (14). У LiF при увеличении τ с 0,7 до 10 кгс/мм2 v возрастает на десять порядков (примерно с 10-6 до 104 см/с). На сплаве железа с 3,25% Si при сравнительно небольшом увеличении касательного напряжения (менее чем в два раза) также обнаружено резкое возрастание скорости движения краевых дислокаций от очень малых значений (порядка 10-7—10-8 см/с) до больших (порядка 10-2 см/с). У германия же зависимость v от τ выражена несравненно слабее.
Скорость скольжения дислокации не может превышать скорость распространения в данном кристалле упругой деформации, т. е. скорость звука.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 716; Нарушение авторских прав?; Мы поможем в написании вашей работы!