
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Автономное регулирование
|
|
|
|
Качество многомерных систем регулирования можно значительно повысить, если применить различные методы компенсации (или развязывания) перекрестных связей. Это справедливо даже для таких систем, степень связности которых, оцениваемая с помощью матрицы Бристоля, не велика. Среди большого числа способов компенсации перекрестных связей одного из наиболее неизвестных классических, является метод синтеза автономной системы. Рассмотрим понятие автономности на следующем примере. Пусть требуется управлять выходами процесса у(0) с помощью регулирующих воздействий U. Система управления, в состав которой входит ряд отдельных контуров регулирования и компенсатор перекрестных связей, показана на рис. 3. Одномерные регуляторы определяют диагональную структуру передаточной матрицы Gc:,,-,,,-..,
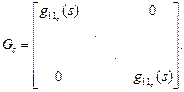 (80)
(80)
Передаточная матрица замкнутой системы с учетом передаточной матрицы компенсатора G; (рис. 3.7) будет задаваться выражением

или 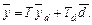 (81)
(81)
Компенсатор G предназначен для ослабления влияния перекрестных связей. В идеальном случае он должен обеспечивать диагональность Т в каждый момент времени
 (82)
(82)
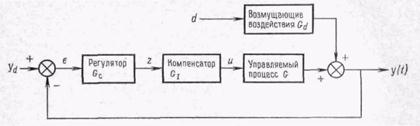
Рис. 4. Многосвязная система регулирования с компенсацией взаимосвязей (автономная система).
или приближение Т к I при t 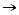
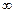 (s
(s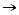 0) при некотором выборе настроек параметров регуляторов. Очевидно, что автономность в этом смысле рассматривается только для случая квадратных матриц G, G/, Gc').
0) при некотором выборе настроек параметров регуляторов. Очевидно, что автономность в этом смысле рассматривается только для случая квадратных матриц G, G/, Gc').
Поскольку матрица Gc диагональна, необходимым условием диагональности Т и предельного соотношения Т(0)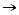 1 при возрастании коэффициентов усиления будет выполнение следующего соотношения:
1 при возрастании коэффициентов усиления будет выполнение следующего соотношения:

или 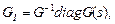 (83)
(83)
где diag G — диагональная матрица, получаемая из G обнулением всех недиагональных элементов.
Если при этом компенсация будет полной, то передаточная матрица замкнутой системы примет вид

или
 i = 1, 2,..., l. (84)
i = 1, 2,..., l. (84)
- Надо отметить, что в этом случае достигается полная автономность по задающим воздействиям, и, несмотря на то что каждое возмущение может влиять на все выходы, эффект возмущения на любой из выходов может быть скомпенсирован отдельным одномерным регулятором gU(,{s).
Иногда бывают случаи, когда осуществить полную динамическую компенсацию слишком сложно или даже невозможно. Напротив, автономность в статике всегда может быть обеспечена таким выбором компенсатора G;, при котором—диагональная матрица (ss — индекс установившегося  состояния):
состояния):
 (85)
(85)
Соответствующая передаточная матрица замкнутойсистемы определяется выражением
 (86)
(86)
При этом оказываются скомпенсированными все перекрестные связи в установившемся состоянии, так что, изменяя коэффициенты усиления отдельных регуляторов, можно повысить качество системы. Однако даже в этой благоприятной ситуации в переходном процессе возможен период заметного влияния динамических связей, вследствие чего отдельные регуляторы могут действовать на объект в противоположных направлениях. По этой же причине, особенно если настройки регуляторов выбраны слишком жесткими, нежелательны большие значения интегральных составляющих ПИД-законов.
Вышеизложенное рассмотрение проводилось для обратных связей по выходам. Если все состояния процесса измеряются непосредственно или могут быть оценены, то для создания автономной системы регулирования можно использовать и обратные связи по состояниям.
Применим разобранную методику синтеза к следующей модельной задаче управления.
Пример. Вернемся к дистилляционной колонне, рассмотренной в примере 8, и рассмотрим для нее задачи синтеза статической и динамической автономных систем регулирования. Статическая автономность достигается выбором передаточной матрицы  в виде
в виде 
или 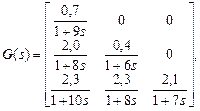 ( 87)
( 87)
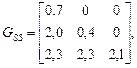
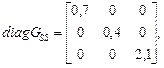 (88)
(88)
 1
1
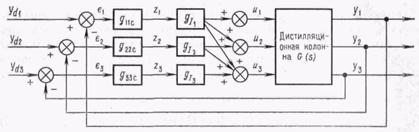
Рис. 3. Автономная система регулирования для дистилляционной колонны.
откуда получаем

Автономная система регулирования, не учитывающая влияния возмущений, показана на рис. 8. Статическая автономность достигается за счет выбора коэффициентов усиления компенсатора в виде
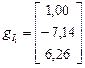 ,
, 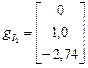 ,
,  (89)
(89)
Динамический компенсатор определяется по формуле
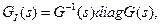 где
где

 (90)
(90)
В соответствии с этим получаем для G(s) и его блоков gJt(s), gj2{s), glt(s) выражения



 (91)
(91)
Отметим, что для динамической компенсации требуется дифференцирование сигналов, связывающих отдельные контуры регулирования. Более подробно качество процессов в статической и динамической автономных системах для данного примера будет описано в гл. 6.
Автономное регулирование не всегда оказывается столь эффективным, как в рассмотренном только что примере. Так, если передаточная матрица G(s) содержит элементы чистого запаздывания, динамический компенсатор, как правило, должен включать элементы опережения, использующие будущие значения выходов. Очевидно, что элементы опережения в чистом виде не могут быть реализованы, однако часто удается получить неплохие результаты, используя вместо них различные прогнозаторы.
Другим существенным моментом является необходимость точно знать передаточную матрицу объекта. Как правило, однако, вместо точной модели процесса G* при синтезе системы регулирования используется приближенная модель G, в результате чего получается передаточная функция замкнутой системы вида
 (92)
(92)
Если при этом точная и приближенная модели объекта G* и G значительно отличаются друг от друга, то качество регулирования будет плохим и замкнутая система может даже стать неустойчивой.
Вопросы устойчивости особенно важны в том случае, когда передаточная матрица объекта имеет нули в правой полуплоскости. Эти нули оказываются неустойчивыми полюсами G, [согласно (83)], и их неточная компенсация приводит к тому, что в передаточной матрице замкнутой системы появляются неустойчивые полюса.
Еще одним потенциально слабым местом автономных систем регулирования является возможное ухудшение динамических характеристик замкнутой системы при компенсации перекрестных связей. В тех случаях, когда перекрестные связи улучшают динамику системы, следует применять такие приемы регулирования, которые сохраняли бы эти полезные свойства. Некоторые из этих приемов будут рассмотрены ниже.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1562; Нарушение авторских прав?; Мы поможем в написании вашей работы!