Примеры игр

Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш, независимо от того, какие стратегии применяет противник.

Терминология и классификация игр

В теории игр предполагается, что игра состоит из ходов, выполняемых игроками одновременно или последовательно.

Ходы бывают личными и случайными. Ход называется личным, если игрок сознательно выбирает его из совокупности возможных вариантов действий и осуществляет его (например, любой ход в шахматной игре). Ход называется случайным, если его выбор производится не игроком, а каким-либо механизмом случайного выбора (например, по результатам бросания монеты).

Совокупность ходов, предпринятых игроками от начала до окончания игры, называется партией.

Одним из основных понятий теории игр является понятие стратегии. Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от ситуации, сложившейся в процессе игры. В простых (одноходовых) играх, когда в каждой партии игрок может сделать лишь по одному ходу, понятие стратегии и возможного варианта действий совпадают. В этом случае совокупность стратегий игрока охватывает все возможные его действия, а любое возможное для игрока i действие является его стратегией. В сложных (многоходовых играх) понятие «варианта возможных действий» и «стратегии» может отличаться друг от друга.

Возможно, что стратегия, обеспечивающая максимальный выигрыш, не обладает другим важным представлением оптимальности, как устойчивостью (равновесностью) решения. Решение игры является устойчивым (равновесным), если соответствующие этому решению стратегии образуют ситуацию, которую ни один из игроков не заинтересован изменить.

Повторим, что задача теории игр - нахождение оптимальных стратегий.

Классификация игр представлена на рис. 1.1.

1. В зависимости от видов ходов игры подразделяются на стратегические и азартные. Азартные игры состоят только из случайных ходов - ими теория игр не занимается. Если наряду со случайными ходами есть личные ходы, или все ходы личные, то такие игры называются стратегическими.

2. В зависимости от числа участников игры подразделяются на парные и множественные. В парной игре число участников равно двум, в множественной - более двух.

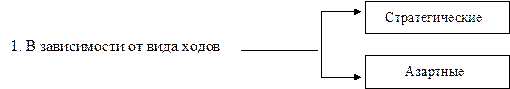
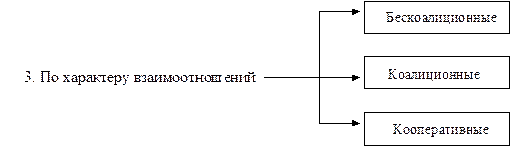
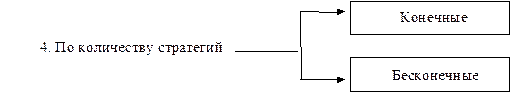
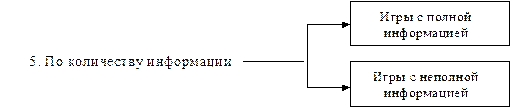
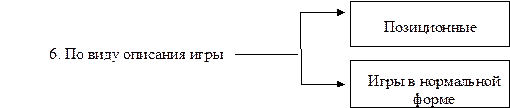
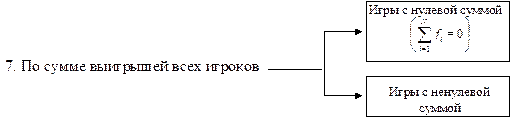
Рис. 1.1. Классификация игр

5. По количеству информации, имеющейся у игроков относительно прошлых ходов, игры подразделяются на игры с полной информацией (имеется вся информация о предыдущих ходах) и неполной информацией. Примерами игр с полной информацией могут быть шахматы, шашки и т.п.

7. Если любая возможная партия некоторой игры имеет нулевую сумму выигрышей f _i, всех N игроков (), то говорят об игре с нулевой суммой. В противном случае игры называются играми с ненулевой суммой.

Очевидно, что парная игра с нулевой суммой является антагонистической, так как выигрыш одного игрока равен проигрышу второго, а следовательно цели этих игроков прямо противоположны.

Конечная парная игра с нулевой суммой называется матричной игрой. Такая игра описывается платежной матрицей, в которой задаются выигрыши первого игрока. Номер строки матрицы соответвует номеру применяемой стратегии первого игрока, столбец - номеру применяемой стратегии второго игрока; на пересечении строки и столбца находится соответствующий выигрыш первого игрока (проигрыш второго игрока).

Конечная парная игра с ненулевой суммой называется биматричной игрой. Такая игра описывается двумя платежными матрицами, каждая для соответствующего игрока.

Игра 1. Зачет

Пусть игрок 1 - студент, готовящийся к зачету, а игрок 2 - преподаватель, принимающий зачет. Будем считать, что у студента две стратегии: А₁- хорошо подготовиться к зачету; А₂ - не подготовиться. У преподавателя имеется тоже две стратегии: В₁ - поставить зачет; В₂ - не поставить зачет. В основу оценки значений выигрышей игроков можно положить, например, следующие соображения, отраженные в матрицах выигрышей

	В1	В2			В1	В2
А1	+ (5) (оценили по заслугам)	- (-6) (обидно)		А1	+ (0) (все нормально)	- (-3) (проявил несправедли вость)
А2	(1) (удалось словчить)	(0) (получил по заслугам)		А2	-2 (дал себя обмануть)	- 1 (студент придет еще раз)
Выигрыши студента	Выигрыши преподавателя

Данная игра в соответствии с приведенной выше классификацией является стратегической, парной, бескоалиционной, конечной, описана в нормальной форме, с ненулевой суммой. Более кратко данную игру можно назвать биматричной.

Задача состоит в определении оптимальных стратегий для студента и для преподавателя.

Игра 2. Морра

Пусть два игрока «выбрасывают» одновременно один, два или три пальца. При четной сумме выигрывает первый игрок, при нечетной – второй. Выигрыш равен сумме «выброшенных пальцев». Таким образом, в данном случае каждый из игроков имеет по три стратегии, а матрица выигрышей первого игрока (проигрышей второго) имеет вид:

	В1	В2	В3
А1		-3
А2	-3		-5
А3		-5

где А _i – стратегия первого игрока, заключающаяся в «выбрасывании» i пальцев;

В _j – стратегия второго игрока, заключающаяся в «выбрасывании» j пальцев.

Что должен делать каждый из игроков, чтобы обеспечить себе максимальный выигрыш?

Дата добавления: 2014-01-07