Базис И, ИЛИ, НЕ. Свойства элементарных функций алгебры логики

Пусть x - некоторая логическая переменная. Тогда:

1. 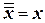, что означает возможность исключения из логического выражения всех членов, имеющих двойное отрицание, заменив их исходной величиной;

2. 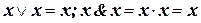- правила подобных преобразований, которые позволяют сокращать длину логических выражений;

3. x Ú0= x;

4. x Ú1=1;

5. x ^. 0=0;

6. x ^. 1= x;

7. ;

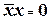8. .

Дизъюнкция и конъюнкция обладают рядом свойств, аналогичных свойствам обычных арифметических операций сложения и умножения:

1). свойство ассоциативности (сочетательный закон):

x₁ Ú(x₂ Ú x₃)=(x₁ Ú x₂) Ú x₃, x₁(x₂ x₃)=(x₁ x₂) x₃;

2). свойство коммутативности (переместительный закон):

x₁ Ú x₂ = x₂ Ú x₁, x₁x₂=x₂ x₁;

3). свойство дистрибутивности (распределительный закон):

для конъюнкции относительно дизъюнкции

x₁ &(x₂ Ú x₃)=(x₁ & x₂) Ú(x₁&x₃);

для дизъюнкции относительно конъюнкции

x₁ Ú x₂ & x₃ =(x₁ Ú x₂) &(x₁ Ú x₃).

Свойство дистрибутивности фактически определяет правила раскрытия скобок или взятия в скобки логических выражений.

Справедливость указанных свойств легко доказывается с помощью вышеизложенных аксиом.

Докажем, например, что

x₁ Ú x₂ & x₃ =(x₁ Ú x₂) &(x₁ Ú x₃).

В самом деле, (x₁ Ú x₂)(x₁ Ú x₃) = x₁x₁ Ú x₁x₃ Ú x₁x₂ Ú x₂x₃ = x₁ Ú x₁x₂ Ú x₁x₃ Ú Úx₂x₃ = x₁( 1Ú x₂ Ú x₃) Ú x₂x₃.

Аналогично можно доказать и другие законы.

Таким же образом доказывается правильность соотношений, известных как законы де Моргана:

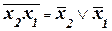, (5)

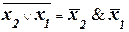. (6)

Из законов де Моргана следует, что:

. (7)

, (8)

помощью которых появляется возможность выражать конъюнкцию через дизъюнкцию и отрицание или дизъюнкцию через конъюнкцию и отрицание.

Законы де Моргана и следствия из них справедливы для любого количества переменных:

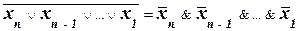, (9)

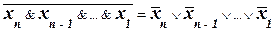. (10)

Для логических функций устанавливаются соотношения, известные как законы поглощения:

x₁ Ú x₁x₂ = x₁, (11)

x₁ &(x₁ Ú x₂) = x₁. (12)

Очень важными в теории ФАЛ являются действия полного склеивания и неполного склеивания. Примеры выполнения этих действий с двумя конституентами 1 приведены ниже:

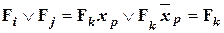- полное склеивание; (13)

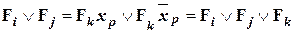- неполное склеивание. (14)

Более важным для практики является неполное склеивание, так как для сложных ФАЛ исходные конституенты 1 F _i и F _j после получения результата склеивания друг с другом F _k сохраняются для сопоставления с другими минтермами в записи заданной ФАЛ и нового склеивания по одной из переменных, входящих в сопоставимые минтермы с отрицанием и без отрицания (отличающихся по одной переменной).

Рассмотренные основные соотношения позволяют описать равносильные булевы функции различными способами, вследствие чего открываются возможности выбора самых простых форм описания ФАЛ. Самые простые по форме ФАЛ реализуются на элементной базе по принципиальным схемам, имеющим самую низкую стоимость.

Дата добавления: 2014-01-07