Минимизация с помощью минимизирующих карт

Минимизация функций алгебры логики

Как было отмечено выше, одним из способов представления ФАЛ от небольшого числа переменных (обычно не больше 5) являются диаграммы Карно или Вейча, которые строятся на развёртках многомерных кубов на плоскость. При этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта заполняется путём пометки кодов вершин, соответствующих наборам, на которых ФАЛ равна единице. Другими символами помечаются коды наборов, на которых ФАЛ не определена. Таким образом, диаграмма на карте Карно или Вейча соответствует представлению ФАЛ в СДНФ.

Пример диаграммы Вейча функции пяти переменных представлен на рис.9. По этим диаграммам находятся соседние наборы переменных, на которых ФАЛ равна 1 (или не определена). Соседние на карте наборы переменных отличаются по одной переменной и могут быть по ней склеены, с исключением из наборов этой переменной. Последовательное применение неполного склеивания к наборам, образующим сплошные поля из двух, четырёх, восьми, шестнадцати и. т. д. наборов, на которых ФАЛ равна единице, позволяет исключить одну, две, три, четыре и. т. д. переменных из этих наборов, то есть минимизировать эту ФАЛ. Эти поля должны быть симметричными относительно соединительной линии карт меньшей размерности. На рис.9. такие поля описываются как пересечение полей постоянных значений переменных в наборах. Поле из наборов переменных 2-0-4-6-26-24-20-22 описывается пересечением полей постоянных значений переменных 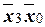, поле из наборов переменных 2-12-22-32 описывается пересечением полей постоянных значений переменных , поле из наборов переменных 4-14-24-34 описывается пересечением полей постоянных значений переменных . Таким образом, минимизированная ФАЛ, приведенная на рис.9, записывается в дизъюнктивной нормальной форме (ДНФ) как

F=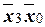Ú Ú 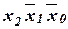. (24)

Отсюда видно, что минимизированная ФАЛ имеет гораздо более простую форму записи, чем исходная функция.

Из рис.9 видно, что на 20₈ (индекс 8 - указание на основание системы счисления) наборе следует придать единичное значение минимизируемой функции, а на 16₈ наборе доопределить ФАЛ как имеющую нулевое значение.

Дата добавления: 2014-01-07