Сила осадки

Участок застоя.

Подставляя в уравнение равновесия

,

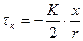и имеем (принимаем r=h, см. выше)

,

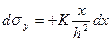Откуда

Константу С находим из условия равенства нормальных напряжений на стыке зон застоя и торможения при x = r (радиус зоны застоя, как указывалось ранее, примерно равен h):

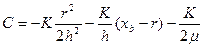
Как видно, давление металла на бойки s_y в крайних точках контактной площадки равно пределу текучести материала К, а затем нарастает к середине и может значительно превышать предел текучести. Эпюра давления представляет собой изменение сопротивления деформации металла по контактной площадке. На этом примере удобно продемонстрировать различие терминов «предел текучести» и «сопротивление деформации». Предел текучести материала получается в условиях равномерной деформации образца, то есть при отсутствии сил трения. Если при осадке исключить трение на контакте, то представленная выше эпюра напряжений s_y превратится в горизонтальную линию, и по всей площади контакта давление s_y будет равно пределу текучести (с учётом вида напряжённого состояния) К (рис 36, штриховая линия). С ростом сил трения купол эпюры увеличивается. В каждой точке этой кривой нормальное напряжение s_y

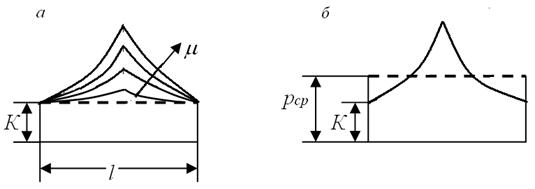
Рис. 36. Влияние сил трения на эпюру нормальных давлений (а) и определение среднего давления (б)

также представляет собой некоторый предел текучести в том смысле, что при таком, а не меньшем, напряжении металл переходит из упругого состояния в пластическое. Но это напряжение называется сопротивлением деформации. Таким образом, сопротивление деформации характеризуется напряжением, при котором металл начинает пластически деформироваться в реальных условиях. На высоких очагах деформации сопротивление деформации отличается от предела текучести из-за неравномерности деформации по высоте. На низких – из-за действия сил трения на контакте.

Так как давление металла на инструмент при осадке переменно во времени (из-за изменения высоты) и изменяется сложно, то для практических задач используется среднее давление р_ср, которое вычисляется путем усреднения наряжения s_y по ширине площади контакта b:

.

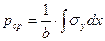(в общем случае, интегрирование и усреднение надо вести по площади контакта, но при плоской деформации размер l по координате z можно не учитывать или положить l=1 м)

На рис 36,б представлена усредненная эпюра s_y = р_ср (площадь под ней равна площади под эпюрой s_y). Видно, что среднее давление превышает предел текучести К, и это превышение можно оценить коэффициентом подпора, учитывающим влияние контактных сил трения,

.

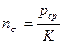Естественно, при отсутствии сил трения n_s = 1, и по мере роста сил трения n_s возрастает.

Полная сила, действующая на боек, равна

Р = р_ср× bl.

Глава 3. Очаг деформации при продольной прокатке

Дата добавления: 2014-01-07