Непрерывные случайные величины. Функция распределения случайной величины. Опр. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка

Опр. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно (несчетно).

Примеры. 1. Расстояние от точки попадания до центра мишени.

2. Размер детали, выпускаемой на данном станке.

Для дискретной случайной величины исчерпывающей характеристикой является ряд распределения (таблица распределения).

Непрерывная случайная величина имеет бесконечное множество возможных значений, сплошь заполняющих некоторый промежуток. Значит для непрерывной случайной величины в отличии от дискретной невозможно составить таблицу распределения, в которой были бы перечислены все возможные значения.

Наиболее общей формой закона распределения, пригодной для всех случайных величин является функция распределения.

Опр. Функцией распределения случайной величины X называется вероятность того, что случайная величина X примет значение, меньше, чем заданное x:

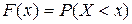. (1)

Геометрически: [вероятность того, что случайная точка X попадет левее заданной точки x ]

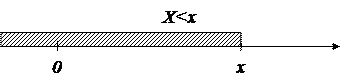F(x) – вероятность того, что случайная величина X примет значение, которое изобразится на числовой оси точкой, лежащей левее заданной точки x.

Функцию распределения F(x) иногда называют «интегральной функцией распределения».

Дата добавления: 2014-01-07