Центральная предельная теорема

Данная теорема определяет условия, при которых возникает СВ с нормальным законом распределения – т.е. закон распределения суммы большого числа СВ 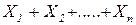близок к нормальному.

Эта теорема впервые была сформулирована русским математиком Ляпуновым А.М. (1857-1918).

Одна из простейших форм – относится к случаю одинаково распределенных слагаемых.

Теорема. Если X₁…X_n-случайные независимые величины имеющие одно т тоже распределение с математическим ожиданием m и дисперсией σ², то при увеличении n закон распределения суммы

неограниченно приближается к нормальному.

Теорема Ляпунова. Пусть X₁, …,X_n – независимые случайные величины с математическими ожиданиями m₁, …, m_n и дисперсиями D₁, …, D_n, причем при n→∞

.

При наличии данных условий закон распределения

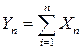
неограниченно стремится к нормальному при n ®¥

Например, теоремы Муавра–Лапласа – частный случай ЦПТ. Если производится m независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение:

Упрощенный вариант – Если СВ есть сумма большого числа независимых СВ, влияние которых на всю сумму мало, то Х имеет закон распределения, близкий к нормальному.

Пример1.2. Требуется произвести 60 выплат. Размер выплат случаен, но средняя выплата равна 50, а средне квадратичное отклонение равно 20.

1. Сколько должно быть денег в кассе, чтобы с вероятностью 0Б95 хватило всем?

2. Сколько денег с вероятностью 0,95 останется в кассе, если первоначально было 3500.

Решение. Суммарная выплата . На основании центральной предельной теореме для одинаково распределенных слагаемых Y имеет приблизительно нормальное распределение с параметрами

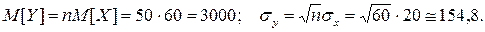
Необходимый запас определяем с использованием функции Лапласа:

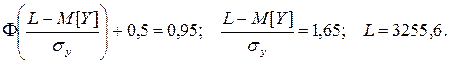
Остается

3500-3255,6=244.4.

Дата добавления: 2014-01-07