Доверительный интервал для математического ожидания

Пусть по выборке достаточно большого объема, n > 30, и при заданной доверительной вероятности 1– a необходимо определить доверительный интервал для математического ожидания m_x, в качестве оценки которого используется среднее арифметическое

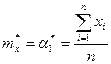
Закон распределения оценки математического ожидания близок к нормальному (распределение суммы независимых случайных величин с конечной дисперсией асимптотически нормально).

Если потребовать абсолютную надежность оценки математического ожидания, то границы доверительного интервала будут бесконечными [– ∞, +∞]. Выбор любых более узких границ связан с риском ошибки, вероятность которой определяется уровнем значимости a. Интерес представляет максимальная точность оценки, т.е. наименьшее значение интервала. Для симметричных функций минимальный интервал тоже будет симметричным относительно оценки m_x. В этом случае выражение для доверительной вероятности имеет вид

P(| m*_x – m_x | < ε) = 1– a,

где ε – абсолютная погрешность оценивания.

Нормальный закон полностью определяется двумя параметрами – математическим ожиданием и дисперсией. Величина m^*_x является несмещенной, состоятельной и эффективной оценкой математического ожидания, поэтому ее значение принимаем за значение математического ожидания. Определим оценку дисперсии случайного параметра m^*_x, учитывая, что этот параметр равен среднему арифметическому одинаково распределенных случайных величин x_i (следовательно, их дисперсии D(x_i) одинаковы и равны S ²)

.

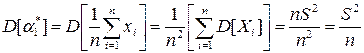Итак, случайная величина m^*_x распределена по нормальному закону с параметрами m^*_x и S²/n. Для установления необходимых соотношений целесообразно перейти к центрированным и нормированным величинам. Выражение m^*_x – m_x можно трактовать как центрирование случайной величины m^*_x. Нормирование осуществляется делением на величину среднеквадратического отклонения оценки m^*₁

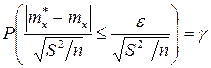
Для стандартизованной величины вероятность соблюдения неравенства определяется по функции нормального распределения

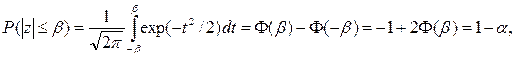
где 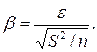Значение β равно квантили u_1–a/2 стандартного нормального распределения уровня 1– a /2. В частности, уровням надежности 0,9, 0,95 и 0,99 соответствуют значения допустимого отклонения u_{1– a/2} величины z, равные 1,64, 1,96 и 2,58 соответственно. Окончательно можно записать

u ²_{1– a/2} = nε²/m^*_x. (4.1)

Нетрудно заметить, что это выражение аналогично по своему содержанию формуле, полученной с использованием общего метода построения доверительного интервала.

При фиксированном объеме выборки из (4.1) следует, что чем больше доверительная вероятность 1– a, тем шире границы доверительного интервала (тем больше ошибка в оценке математического ожидания). Это равенство позволяет определить необходимый объем выборки для получения оценки математического ожидания с заданной надежностью и требуемой точностью (погрешностью):

n=S²u²_{1– a/2}/ε ².

Если перейти к относительной погрешности ε₀ = ε/ m^*_x, то

n = S² u²_{1– a/2} /( ε₀ ² m^*_x²). (4.2)

Таким образом, чтобы снизить относительную погрешность на порядок, необходимо увеличить объем выборки на два порядка. Приведенная формула часто используется в статистическом моделировании для определения необходимого количества испытаний модели.

Во многих случаях предположение о нормальном распределении случайной величины m^*_x становится приемлемым при n > 4 и вполне хорошо оправдывается при n >10. Оценка m^*_x вполне пригодна для применения вместо m_х. Но не так обстоит дело с дисперсией, правомочность ее замены на S² не обоснована даже в указанных случаях. При небольшом объеме выборки, n < 30, закон распределения оценки дисперсии S² принимать за нормальный неоправданно. Ее распределение следует аппроксимировать распределением хи-квадрат как суммы квадратов центрированных величин (хи-квадрат распределение сходится к нормальному при количестве слагаемых, превышающем 30). Но это утверждение обосновано только для случая, когда случайная величина Х распределена нормально.

С учетом сделанных допущений величина z будет подчиняться закону распределения Стьюдента с n –1 степенями свободы (одна степень свободы использована для определения оценки дисперсии). Распределение Стьюдента симметричное, поэтому полученное соотношение между точностью, надежностью оценки и объемом выборки сохраняется, меняются только значения квантилей. Вместо квантили нормального распределения u_{1– a/2} следует взять квантиль t_{1– a/2(n–1)} распределения Стьюдента с (n –1) степенями свободы. Значения критических точек распределения Стьюдента для некоторых вероятностей и различных степеней свободы, представлены в таблицах. Сравнение таблиц показывает, что квантили распределения Стьюдента больше квантилей нормального распределения того же уровня надежности при малом n. Иначе говоря, применение нормального распределения при небольшом объеме выборки ЭД приводит к неоправданному завышению точности оценки.

Пример 4.2. Определить с надежностью g = 0,9 доверительный интервал для математического ожидания случайной величины с точечными оценками m^*_х =27,51 и S² =0,91, n = 44.

Решение. Интервал двусторонний, симметричный a = 0,1. Объем выборки можно считать большим, поэтому воспользуемся нормальным распределением, тогда u_0,95 = 1,96. Допустимое отклонение

ε = u_0,95(m^*₂ /n)^0,5 =1,96 (0,91/44)^0,5 = 0,28.

С вероятностью 0,9 НДГ интервала составит θ ₀ =27,51– 0,28=27,23, ВДГ интервала θ ₁ = 27,51 + 0,28 = 27,79.

Другими словами, с вероятностью 0,9 значение математического ожидания лежит в пределах от 27,23 до 27,79.

Пример 4.3. Определить с надежностью g = 0,9 (a = 0,1) доверительный интервал для математического ожидания случайной величины с точечными оценками m^*_х = 55 и S² = 658,6. Объем выборки n =6

Решение. Объем выборки n=6 нельзя считать большим, поэтому воспользуемся распределением Стьюдента при числе степеней свободы, равном 5. Тогда для двусторонней критической области в соответствии с табл. Функции Стьюдента допустимое отклонение стандартизованной случайной величины составит

t_0,9(4)=t(5; 0,1)= 2,015.

Допустимое отклонение исходной величины составит

ε= t_0,9(5)(m^*₂ /n) 0,5 =2,015 (658,6/6)0,5 = 21,11.

Границы интервала: θ ₀ =55–21,11=33,89 и θ ₁ =55+21,11= 76,11.

В данном примере использование нормального распределения вместо распределения Стьюдента приведет к неоправданному сужению интервала в 2,015/1,64 = 1,3 раза.

Дата добавления: 2014-01-07