Матрица данных

КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ

Многие объекты исследования характеризуются множеством параметров, и по результатам наблюдения за их функционированием формируются многомерные совокупности (матрицы) ЭД

(7.1)

Строки такой матрицы соответствуют результатам регистрации всех наблюдаемых параметров объекта в одном эксперименте, а столбцы содержат результаты наблюдений за одним параметром (фактором, вариантой) во всех экспериментах. Обозначим количество параметров через m(m>1), а количество наблюдений – через n.

В матрице элемент х_ij соответствует значению j -й варианты в i -м наблюдении. Матрица, вообще говоря, может содержать пустые значения некоторых элементов, например, из-за пропусков в регистрации значений параметров. В многомерном анализе желательно устранить пропущенные значения. Для этого существуют специальные приемы, в частности, вычеркивание соответствующих строк матрицы или занесение средних значений вместо отсутствующих. В дальнейшем будем считать, что матрица не содержит пустых элементов, а параметры объекта характеризуются непрерывными случайными величинами.

Методы обработки матрицы ЭД основаны на следующем предположении: если объект подвергнуть новому обследованию и получить, вообще говоря, другую матрицу данных, то после ее обработки с помощью тех же методов будут получены результаты, близкие к результатам обработки первой матрицы. Данное предположение основано на статистической гипотезе формирования матрицы ЭД. Матрица порождается случайным образом в соответствии с определенной вероятностной закономерностью, а именно: в m -мерном пространстве параметров существует некоторое (пусть и неизвестное) распределение вероятностей, и каждая строка матрицы появляется в соответствии с этим распределением независимо от появления других строк.

Каждый столбец матрицы представляет собой случайную выборку значений одного параметра объекта. Указанное предположение означает, во-первых, что оценки моментов и параметров распределения, вычисленные по выборке, будут близки к истинным значениям, во-вторых, значения непрерывных функций, построенных по этим оценкам, будут близки к значениям функций, построенным по истинным значениям параметров.

Таким образом, объектом исследования в многомерном анализе является многомерная случайная величина, представленная выборкой конечного объема. К такой выборке применимы все методы и оценки, рассмотренные при обработке одномерных ЭД. Конечно, приведенные суждения не являются доказательством допустимости применения рассматриваемых методов, но вполне подтверждаются практикой.

Параметры, характеризующие объект исследования, имеют разныйфизический смысл, и матрица данных существенно изменяется, если изменяются шкалы, в которых измеряются те или иные параметры. Матрицу данных еще до проведения анализа целесообразно привести к стандартному виду, т.е. стандартизовать значения вариант (напомним, что среднее значение стандартизованной варианты равно нулю, дисперсия – единице). В тех случаях, когда все варианты измеряются в одной шкале, это преобразование все-таки желательно, ибо оно упрощает последующие преобразования. Стандартизованную матрицу будем обозначать через U. Переход от исходной к стандартизованной матрице осуществляется следующим образом.

1. По каждой варианте вычисляются оценки:

· математического ожидания ;

· дисперсии .

2. Вычисляются элементы стандартизованной матрицы

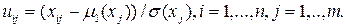
Элементы матрицы U являются безразмерными величинами. Именно матрица U будет являться объектом последующей обработки.

Дата добавления: 2014-01-07