Законы трения

1. Сила трения скольжения направлена противоположно возможному движению тела.

2. Сила трения не зависит от площади соприкасающихся поверхностей.

3. Максимальная сила трения пропорциональна нормальному
давлению. Под нормальным давлением понимают полное давле­ние на всю площадь соприкосновения трущихся поверхностей:

.

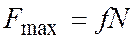4.Коэффициент трения скольжения зависит от материала и
физического состояния трущихся поверхностей.

Многие задачи на равновесие тела на шероховатой поверхно­сти при наличии силы трения, удобно решать геометрически. Для этой цели используют понятие угла и конуса трения.

Пусть твёрдое тело под действием активных сил находится на шероховатой поверхности в пре­дельном состоянии равновесия, т.е. таком состоянии, когда сила трения достигает своего наиболь­шего значения при данном значе­нии нормальной реакции (рис. 8.4). В этом случае полная реакция ше­роховатой поверхности 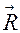отклоне­на от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол.

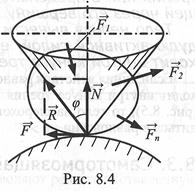
Угол φ между полной реакцией шероховатого тела и направлением нормальной реакции называ­ют углом трения. Угол трения φ зависит от коэффициента тре­ния, т.е.

Но, по закону Ш. Кулона,

F=ƒN, следовательно, tgφ=ƒ, т.е. тангенс угла трения равен ко­эффициенту трения скольжения.

Конусом трения называют конус, описанный полной ре­акцией вокруг направления нормальной реакции. Его можно по­лучить, изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся по­верхностей. Если коэффициент трения во всех направлениях оди­наков, то конус трения круговой.

Если неодинаков, то конус трения не­круговой, например в случае, когда свой­ства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на стро­гальном станке и т.п.).

Для равновесия тела на ше­роховатой поверхности необхо­димо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или в предельном состоянии по его образую­щей через его вершину (рис. 8.5).

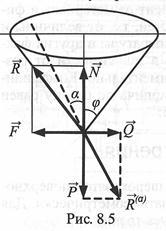
Тело нельзя вывести из равновесия любой по мо­дулю активной силой, если её линия действия про­ходит внутри конуса трения, т.е. α <φ.

Если линия действия равнодействующей активных сил не про­ходит внутри конуса трения или по его образующей, т.е. α> φ (рис. 8.5), то тело на шероховатой поверхности не может нахо­диться в равновесии, Q> F.

Задача 1. Определить модуль силы 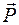, при которой начнется движение блока (рис. 6.7, а). Вес блока Q = 2 кН, высота h = 0,8 м, ширина b = 0,6 м. Сила 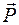, приложенная в точке В, образует угол 30° с горизонтом. Коэффициент трения между блоком и горизон­тальным полом f = 0,2.

Решение. Движение блока может начаться в двух случаях: а) если начнется скольжение блока по плоскости вправо (рис. 6.7, б) и б) если блок начнет опрокидываться вокруг ребра (рис. 6.7, в).

Рассмотрим первый случай. В этом случае точка приложения реакции пола 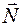неизвестна. Составим уравнения равновесия — при­равняем суммы проекций всех сил на оси координат (рис. 6.7, б) нулю

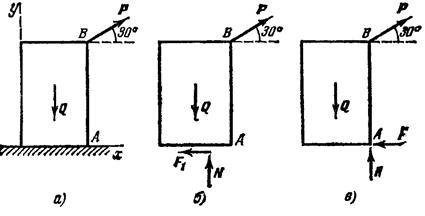
Рис. 6.7

, .

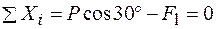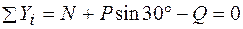Кроме того, учтем зависимость силы трения от нормального дав­ления

.

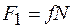Определим из данной системы уравнений силу 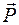. Исключая силы 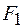и 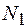, находим

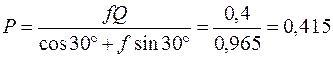кН.

Если величина силы 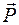станет больше этого значения,то блок нач­нет скользить вправо.

Рассмотрим второй случай. В случае возможного опрокидыва­ния блока вокруг ребра А нормальная реакция 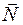и сила трения 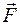будут приложены в точке А (рис. 6.7, в).

Составим три уравнения равновесия и четвертое уравнение-зависимость силы трения от нормального давления:

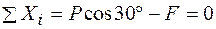, (6.1)

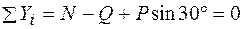, (6.2)

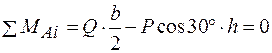. (7.3)

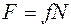. (6.4)

Для нахождения величины силы 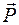достаточно найтиее значение из (6.3):

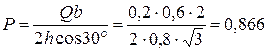кН.

Если модуль силы 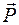станет больше этого значения, то блок начнет опрокидываться около ребра А.

Уравнения (6.1), (6.2), (6.4) смогут быть использованы для опре­деления нормальной реакции и силы трения.

Сопоставляя значения модуля силы 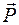в первом и во втором случаях, заключаем, что так как величина силы 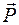при скольже­нии меньше ее величины при опрокидывании, то при возрастании модуля силы 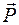от нуля до максимума блок начнетсначала скользить, а не опрокидываться.

2 трение качения

Трение качения возникает в результате деформации катящегося тела и опорной поверхности, которые в действительности не являются абсолютно твердыми. Поэтому контакт между телом и поверхностью происходит по некоторой площадке (рис. 6.8, а). Нормальная реакция смещается относительно центра катка на некоторую величину в сторону движения, которая при выходе тела из равновесия достигает максимума и называется коэффициентом трения качения f_k (рис. 6.8, б).

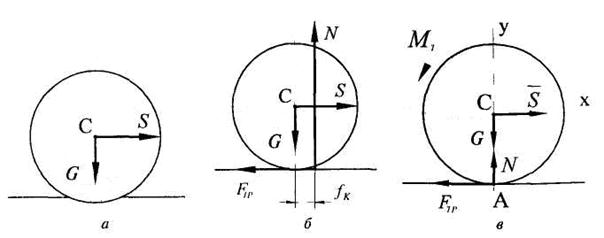
Рис. 6.8

Коэффициент трения качения имеет размерность длины в отличие от безразмерного коэффи­циента трения скольжения. Обычно нормальную реакцию про­водят через центр катка, добавляя при этом к телу пару сил с мо­ментом (рис. 6.9, в), который называют моментом трения качения:

.

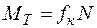Для катка, находящегося в покое, составим три уравнения равновесия (рис. 6.8, в):

1. .

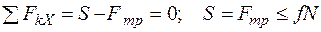2. .

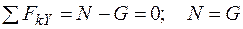3. .

.

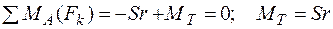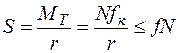Из последнего выражения получим условие качения колеса без скольжения.

Обычно это условие соблюдается. Поэтому для начала каче­ния катка требуется меньшая сила, чем для его скольжения.

Закономерности для момента сопротивления качению:

Дата добавления: 2014-01-07