Лекция 1. (Часть II) Основные определения ЗЛП

Особенности использования агрегатов в условиях крестьянских и других хозяйств новых типов

Эксплуатация машинно-тракторного парка как наука длительное время развивалась в основном применительно к крупным сельскохозяйственным предприятиям — сначала к машинно-тракторным станциям (МТС), а затем (после расформирования МТС) к колхозам и совхозам. Предприятия указанного типа характеризовались огромными площадями сельскохозяйственных угодий, большим количественным составом МТП и значительной численностью механизаторских кадров. Поэтому в определенной степени был оправдан непрерывный рост единичных мощностей и энергонасыщенности тракторов, пропускной способности зерноуборочных и других комбайнов, а также производительности различных сельскохозяйственных машин.

Нарождающиеся в новых условиях крестьянские или фермерские и другие частные хозяйства существенно отличаются от колхозов и совхозов как размерами возделываемых площадей земли, так и численностью работников, определяемой часто количеством взрослых членов семьи. Существенно ограничены и финансовые возможности таких хозяйств.

Указанные особенности, естественно, должны учитываться как при разработке конструкций соответствующих машин и агрегатов, так и при их непосредственной эксплуатации.

Малые объемы работ и ограниченные финансовые возможности диктуют необходимость приобретения малогабаритных агрегатов сравнительно небольшой мощности. Но, с другой стороны, при ограниченной численности работников желательно иметь более высокопроизводительную технику. Необходимо учитывать и то обстоятельство, что при больших единичных мощностях выход из строя (отказ) каждого отдельного агрегата при ограниченном их числе существенно увеличивает вероятность несвоевременного выполнения работ и соответствующего роста количественных и качественных потерь урожая. Совокупность подобных противоречий является характерным признаком для получения оптимального или наилучшего варианта решения.

Методы решения подобных задач находятся лишь на начальной стадии разработки, поэтому их дальнейшее углубленное развитие также представляет собой важное направление развития курса МАШИНОИСПОЛЬЗОВАНИЕ.

В общем виде задачу линейного программирования (ЗЛП) можно записать следующим образом: найти

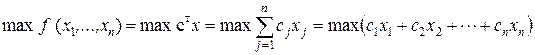
или

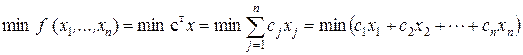
при ограничениях 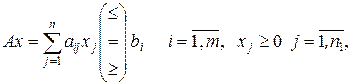где n ₁ £ n.

Здесь

x ^т = (x ₁, x ₂,…, x_n) – n -мерный вектор переменных (план задачи),

c ^т = (c ₁, c ₂,…, c_n) – n -мерный вектор коэффициентов целевой функции,

– матрица коэффициентов левой части системы ограничений,

b ^т = (b ₁, b ₂,…, b_m) – вектор коэффициентов правой части системы ограничений.

Различают две основные формы записи ЗЛП: стандартная и каноническая.

Будем рассматривать в качестве стандартной ЗЛП

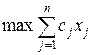, при ограничениях 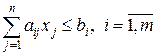, х_j ³ 0, j=,

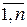каноническая ЗЛП записывается так:

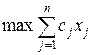, при ограничениях 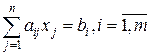, х_j ³ 0, j=.

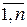От задачи на максимум можно всегда осуществить переход к задаче на минимум и наоборот. Если целевая функция сводится к нахождению min f = c ₁ x ₁ +c ₂ x ₂ +…+ c_nx_n, то можно перейти к задаче нахождения max f ₁ = - f = - c ₁ x ₁ - c ₂ x ₂ -…- c_nx_n, поскольку min f = -max (- f).

Переход от общей ЗЛП к стандартной осуществляется следующим образом.

1. Ограничение-неравенство ЗЛП, имеющее вид «³», можно преобразовать к неравенству вида «£», умножив обе части исходного неравенства на «- 1».

2. Ограничение-равенство a_{i 1} x ₁ +a_{i 2} x ₂ +…+ a_inx_n=b_i можно записать в виде двух неравенств:

.

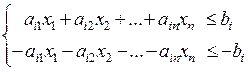3. Если переменная х_k не удовлетворяет условию неотрицательности, т.е.:

а) х_k £ 0, то заменим ее на переменную y_k ³0 такую, что х_k= - y_k;

б) х_k – не определена, то заменим ее на разность двух переменных u_k ³ 0 и v_k ³ 0, приняв x_k = u_k - v_k.

Переход от стандартной ЗЛП к канонической осуществляется путем преобразования ограничений - неравенства вида «£» к строгим равенствам добавлением к левой части неравенства дополнительной переменной, т.е. 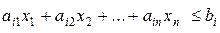преобразуется в неравенство

.

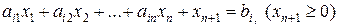Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной стандартной ЗЛП отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в канонической форме, равно объему используемого соответствующего ресурса. Обратный переход от канонической к стандартной форме записи ЗЛП проводится по правилам перехода от общей ЗЛП к стандартной.

Данные формы записи ЗЛП и правила перехода от одной формы к другой имеют практическое значение при решении ЗЛП различными методами, рассматриваемыми ниже. Далее введем основные определения, связанные с решением ЗЛП.

Всякое неотрицательное решение системы ограничений задачи линейного программирования называется планом.

Будем называть любой план задачи линейного программирования допустимым, если он удовлетворяет условиям ограничений задачи.

Допустимый план будем называть опорным, если в нем отличны от нуля не более m+n–1 компонент, а остальные – равны нулю.

Если в опорном плане число отличных от нуля компонент равно в точности n+m-1, то план является невырожденным, иначе – вырожденным.

Допустимый план, при котором целевая функция задачи линейного программирования принимает свое минимальное значение, называется оптимальным планом.

Дата добавления: 2014-01-07