Способы получения критериальных уравнений

Существуют два способа получения критериальных уравнений. Первый из них заключается в преобразовании исходных дифференциальных уравнений математической модели к безразмерному виду. Мы уже применяли этот вид получения критериев подобия в разобранном выше примере. Сформулируем его теперь в общем виде. Его применение заключается в приведении всех членов дифференциального уравнения математической модели к безразмерному виду. Рассмотрим, например, уравнение Эйлера, описывающее поток несжимаемой жидкости в трехмерной системе координат:

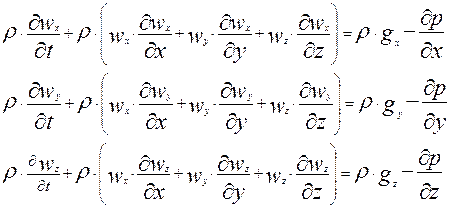(2.10)

Где - r - плотность жидкости, [кг/м³] принимается постоянной величиной; g_x, g_y, g_z – проекции ускорения свободного падения на пространственны оси координат X,Y,Z [м/сек²].

w_x, w_y, w_z – проекции скорости на оси координат, [м/сек]; p – давление [Н], оно убывает вдоль направления потока, что отражает знак минус перед этим слагаемым. Введем для каждой из переменных масштабы изменения этих величин и приведем эти переменные к безразмерному виду. Для скорости в качестве масштаба выберем среднюю скорость потока w_ср, для длины – характерный размер поперечного потока L и заменим размерные переменные в уравнении (2.10) на их относительные безразмерные аналоги:

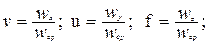- относительные проекции скорости

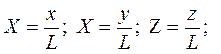- относительные координаты

- относительные проекции ускорения

свободного падения.

Введем также масштаб времени, t₀ и масштаб давления, p_0.

Преобразуем время и давление с использованием этих масштабов:

Подставим в уравнения (2.10) старые переменные, выраженные через их безразмерные аналоги.

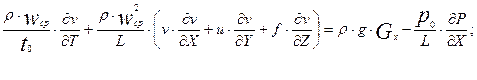(2.11)

По двум остальным уравнениям системы (2.10) будут совершенно аналогичные преобразования, поэтому мы их приводить не будем. Разделим обе части уравнения (2.11) на сомножитель, стоящий перед выражением в скобках в левой части, а именно на величину 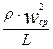. В результате получим следующее уравнение:

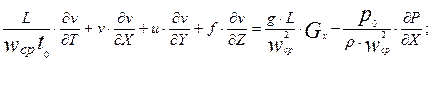(2.12)

Перед всеми слагаемыми полученного уравнения стоят безразмерные комплексы, которые мы обозначим следующим образом:

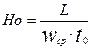- критерий гидродинамической гомохронности Струхаля.

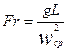- критерий гравитационного подобия Фруда

- критерий подобия полей давления Эйлера.

Подставив эти выражения в уравнение (2.12) мы получим его в следующем виде:

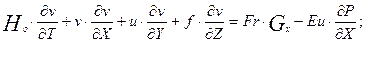(2.13)

Такой метод преобразования уравнений математической модели называется методом нормализации уравнений математической модели системы.

Из уравнения (2.13) прямо вытекают условия подобия модели и объекта: модель и объект обладают подобием течения в них несжимаемой жидкости, если критерии подобия в модели и в объекте равны, т.е. если

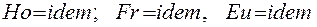
Такой метод составления и подобного преобразования модели и последующего физического моделирования является вполне строгим, однако, для его использования необходимо иметь строгое математическое описание процессов в моделируемом объекте, что не всегда возможно. Для этих случаев применяют обычно метод анализа размерности. Этот метод не требует знания точного математического описания процессов в моделируемом объекте. Для его использования достаточно знания тех определяющих величин, от которых зависит протекание процессов в моделируемом объекте. Все физические величины имеют определенную размерность, выраженную через размерность основных физических величин, принятых за эталоны. Таких основных физических величин 7. Их наименование и размерность приведены в следующей таблице:

Таблица 2.1.Основные величины Международной системы единиц, их размерности и величины.

Величина	Единица
Наименование	Размерность	Наименование	Обозначение
Международное	Русское
	Длина	L	метр	m	м
	Масса	M	килограмм	kg	кг
	Время	Т	секунда	s	c
	Сила электрического тока	I	ампер	А	А
	Термодинами-ческая температура	q	кельвин	К	К
	Количество вещества	N	моль	mol	моль
	Сила света	J	кандала	cd	кд

Приведенные в таблице величины являются первичными. На их основе выражают размерности так называемых вторичных величин с помощью определительных уравнений, выражающих фундаментальные законы природы. Например, размерность скорости получается по определительному уравнению

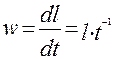(2.14)

Единица силы – ньютон- определяется по второму закону Ньютона:

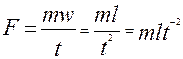(2.15).

Если в формуле размерности числовые коэффициенты равны единице, то систему единиц называют когерентной. Система СИ когерентна.

Формула размерности любой физической величины в СИ имеет следующий вид:

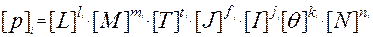(2.16)

где l_i, m_i, t_i, j_i, k_i, f_i, n_i, - показатели степени основных единиц измерения в определительных уравнениях.

Формула размерности любого критерия подобия - безразмерной величины - будет иметь все показатели степени нулевыми:

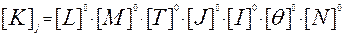(2.17).

С другой стороны, формула размерности критерия, выраженная через размерности производных величин может быть записана следующим образом:

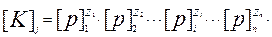(2.18)

С учетом уравнения (2.16) уравнение (2.18) можно записать в следующем виде:

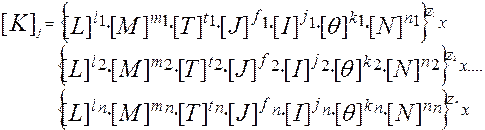(2.19)

Сопоставляя показатели степени при величинах размерностей в уравнениях (2.19) и (2.117) можно записать систему линейных алгебраических уравнений:

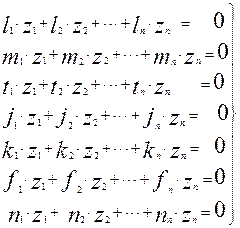(2.20)

Из полученной системы линейных уравнений можно определить все показатели степени z_i критериального уравнения математической модели, считая, что все показатели степени основных размерностей известны. Это допущение вполне оправдано, так как мы всегда знаем физические величины и их размерности, от которых зависит протекание процесса. Если мы из полученной формулы размерностей уберем квадратные скобки, мы получим окончательный вид критериального уравнения.

Методика анализа размерностей предусматривает, что перечень физических величин, существенных для моделируемого объекта, известен и определяется на основе предварительного анализа изучаемого процесса.

В качестве конкретного примера использования метода анализа размерностей, рассмотрим пример анализа системы движения массы тела по закону Ньютона.

Для этой системы существенными физическими величинами, от которых зависит протекание процесса, являются следующие величины:

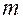· - масса системы ,

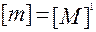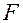· - сила, действующая на систему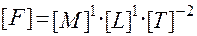

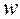· –скорость системы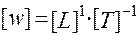

· –время,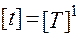

Запишем выражение критерия подобия через вторичные физические величины в следующем виде:

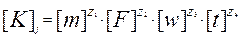(2.21)

и перейдем к записи выражения для критерия через основные физические величины:

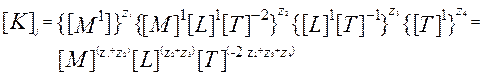(2.22)

Чтобы критерий был безразмерным необходимо соблюдение равенств:

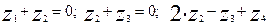(2.23)

Система (2.23) содержит 4 неизвестных в 3-х уравнениях_. Она является недоопределенной и имеет множество решений. Однако это противоречие легко разрешимо. Из системы (2.23) следует, что -z₁=z₂=-z₃ = z₄. Задавая одно из неизвестных: z_i=a, мы получим:

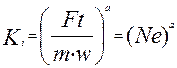(2.24)

Для моделирования достаточно принять: а=1 и соблюдать условие Ne=idem, т.е. мы получили то же самое условие подобия, что и при использовании подобного преобразования уравнения математической модели.

В общем случае использование метода анализа размерностей не так просто, когда в рассмотрении необходимо учитывать большое количество вторичных физических величин. Общее количество уравнений для нахождения показателей степени вторичных физических величин, как это следует из системы, равно R=7 (оно равно числу первичных физических величин). Но все основные физические переменные сразу используются редко, поэтому чаще всего, R<7. При анализе сложных объектов чаще всего оказывается, что общее число вторичных физических величин N_c оказывается больше, N_c>R. В этих случаях система уравнений (2.20) имеет множество решений, причем (N_c-R) этих решений будут независимыми, а все другие будут зависеть от них. Очевидно, что число независимых решений системы (2.20) равно тому минимальному числу критериев подобия, которые нужно получить, чтобы обеспечить грамотное применение моделирования:

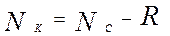(2.25)

Где 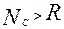в общем случае. Чтобы правильно использовать соотношение (2.25) необходимо учесть все физические величины, оказывающие влияние на моделируемый процесс. Это удается далеко не всегда. Может случиться, что изучаемый процесс подвержен влиянию неких неучтенных величин, и тогда часть критериев подобия оказывается неучтенной, и подобие не может быть обеспечено.

Систему независимых между собой критериев подобия называют фундаментальной. Любой из независимых критериев не может быть выражен через другие независимые критерии с использованием метода анализа размерностей. Любой из зависимых критериев можно выразить через независимые и представить в форме стенной зависимости вида:

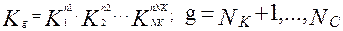(2.26)

Где g>N_K – условный порядковый номер зависимого критерия.

Почти в любой ситуации можно получить несколько наборов N_K независимых между собой безразмерных комплексов. Выяснить какой из этих наборов является «более фундаментальным» для данной ситуации можно только из физических соображений. Для различных физических явлений известны общеупотребительные критерии, которые и стараются включить в число фундаментальных. В таблице 2.2. приведены выражения для наиболее употребительных критериев подобия гидродинамических и тепловых процессов и сформулирован их физический смысл:

№	Критерий	Символ	Наименование	Пояснение
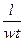
		Но	Критерий гидродинамической гомохронности	Характеризует скорость изменения поля скоростей среды во времени
		Re	Критерий режима движения (число Рейнольдса)	Является мерой отношения сил инерции и молекулярного трения в потоке
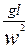
		Fr	Критерий гравитационного подобия (число Фруда)	Мера отношения сил инерции и тяжести в однородном потоке.
		Pe	Критерий теплового подобия (число Пекле)	Мера отношения молекулярного и конвективного переноса тепла в потоке.
		Pr	Критерий подобия температурных и скоростных полей (число Прандлтля)	Мера подобия температурных и скоростных полей в потоке.
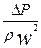
		Ee	Критерий подобия полей давления (число Эйлера)	Мера отношения сил давления и инерции в потоке
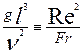
		Ga	Критерий полей свободного течения	Мера отношения сил молекулярного трения и тяжести в потоке. В форме Gr=GabDT характеризует взаимодействие сил молекулярного трения и подъемной силы за счет термического расширения жидкости.
		Fo	Критерий тепловой гомохронности (число Фурье)	Характеризует связь между скоростью изменения температурного поля, физическими свойствами и размерами тела.
9.		Nu	Безразмерный коэффициент теплоотдачи (критерий Нуссельта)	Характеризует связь между интенсивностью теплоотдачи и температурным полем в пограничном слое.
10.		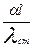Bi	Критерий краевого подобия (критерий Био)	Характеризует связь между полем температур в твердом теле и условиями теплоотдачи на его поверхности.
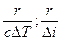
		К	Тепловой критерий фазового превращения	Мера отношения теплового потока, идущего на фазовое превращение к теплоте перегрева (переохлаждения).

Таблица 2.2. Основные критерии подобия гидродинамических и тепловых процессов.

Кроме вышеприведенных критериев иногда применяются также и другие критерии, в зависимости от особенностей представленной задачи.

После формулировки критериального уравнения рассматриваемого процесса необходимо так провести эксперименты на модели, чтобы можно было выполнить определение численных значений показателей степеней в критериальной зависимости типа (2.26). Определив численные значения коэффициентов в критериальной зависимости, можно использовать ее для определения условий функционирования объекта, обеспечивая при этом подобное преобразование условий модели в условия работы объекта. При этом физическая модель выступает в роли своеобразной вычислительной аналоговой машины. При этом мы используем одну из возможных формулировок второй теоремы подобия в следующей формулировке:

Интеграл всякого полного дифференциального уравнения физического процесса можно представить в виде зависимости между критериями подобия, т.е. критериальным уравнением.

Таким образом, применяя теорию подобия можно сформулировать общий вид модели процессов, происходящих в объекте, в виде критериального уравнения, выбрать вид и размеры физической модели объекта, провести исследования на модели, определить численные значения коэффициентов критериального уравнения. Однако такой подход, основанный на физическом моделировании, не всегда приносит хорошие результаты. Среди причин таких результатов можно указать следующие:

1. При использовании теории подобия мы стремимся обеспечить подобное преобразование процесса. Это значит, что условия, полученные на модели, мы стремимся воспроизвести в объекте, Однако условия, оптимальные для процесса в масштабе модели не всегда являются оптимальными для масштаба объекта.

2. Трудно заранее учесть все переменные для получения в достаточном объеме критериального уравнения. Кроме того, уравнение (2.25) накладывает ограничение на количество независимых критериев и часто не позволяет достаточно детально описать сложный процесс с использованием метода анализа размерности.

Поэтому в настоящее время все большее распространение получает метод математического моделирования процессов в объекте. При этом не требуется выполнять подобное преобразование уравнений, описывающих процесс, и использовать затем физическую модель в качестве своеобразной вычислительной машины для получения решения уравнений модели. Возможности современной вычислительной техники позволяют решать сложные системы уравнений, являющиеся детальными математическими моделями процессов в объекте без всяких допущений. При этом можно использовать математические методы оптимизации для определения условий работы объекта с учетом его размеров. Поэтому далее мы рассмотрим методы получения и анализа математических моделей технологических объектов.

Дата добавления: 2014-01-07