К термодинамическим процессам

Первый закон термодинамики, его приложение

Первый закон термодинамики является количественной формулировкой всеобщего закона сохранения энергии применительно к процессам, связанным с превращениями теплоты и работы.

Закон сохранения энергии: энергия не возникает из ничего и не исчезает бесследно; она лишь превращается из одних видов в другие, причем, строго в эквивалентных количествах.

Первый закон термодинамики возник в эпоху создания тепловых двигателей. С появлением тепловых машин перед человечеством встала естественная задача создания экономически выгодных машин. Предпринимались многочисленные попытки создания вечного двигателя I рода − тепловой машины, производящей работу без затрат энергии. Первый закон термодинамики – это постулат; он не может быть доказан логическим путем или выведен из каких-либо более общих положений. Истинность его подтверждается тем, что ни одно из его следствий не находится в противоречии с опытом.

Существует несколько формулировок I закона, например:

– в любой изолированной системе запас энергии остается постоянным;

– невозможно создать вечный двигатель I рода;

– теплота, подведенная к системе Q, расходуется на совершение системой работы A и на увеличение ее внутренней энергии D U:

(1)

Для бесконечно малого изменения состояния системы (в дифференциальной форме)

. (2)

Знак d в уравнении (2) отражает тот факт, что теплота и работа − функции процесса и их бесконечно малое изменение не является полным дифференциалом.

В уравнениях (1) и (2) используется термодинамическая система знаков: теплота положительна, если она передается системе; работа положительна, если она совершается системой.

В общем случае работа является суммой нескольких качественно различных видов работ (механической, электрической, магнитной, поверхностной и др.). В термодинамике принято все виды работы за исключением работы расширения (сжатия) p D V называть полезной работой .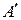

Тогда уравнения (1)-(2) примут вид:

Q = D U + p D V + A¢,

.

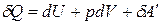Если совершается только работа расширения (сжатия), т.е. A¢ = 0, то

Q = D U + p D V,

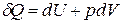. (3)

Практическое значение I закона термодинамики состоит в возможности расчета тепловых эффектов различных процессов и работы, совершаемой системой при их осуществлении.

Применим уравнение (3) к основным термодинамическим процессам.

1) Изохорный процесс (V = const, dV = 0). Так как работа расширения при этом равна 0, то, очевидно, что вся теплота, подведенная к системе, идет на увеличение внутренней энергии:

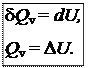
Таким образом, теплота изохорного процесса равна изменению внутренней энергии и, следовательно, является функцией состояния.

2) Изобарный процесс (p = const, dp = 0).

Из математики: любую константу можно внести под знак дифференциала, а сумма дифференциалов равна дифференциалу от суммы.

Уравнение (3) в этом случае запишется в виде

,

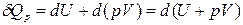где U + pV º H − функция состояния системы, называемая энтальпией.

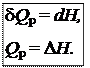
Таким образом, теплота изобарного процесса равна изменению энтальпии и является функцией состояния.

Работа расширения изобарного процесса

А = p D V = p (V ₂ – V ₁),

где V ₁, V ₂ – объем системы в исходном и конечном состояниях.

Если изобарный процесс протекает в идеальном газе, то в соответствии с уравнением Менделеева-Клапейрона для исходного 1 и конечного 2 состояний можно записать:

.

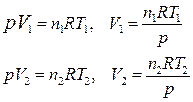Тогда

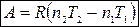(4).

Для изобарно-изотермического процесса (р, Т = const)

Т ₁ = Т ₂ = Т

уравнение (4) запишется:

,

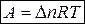где .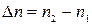

Связь между Q _v и Q _p определяется уравнением:

.

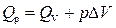Для реакций, протекающих с участием только конденсированных фаз (твердых и жидких), объем системы практически не изменяется (D V = 0) и Q _p» Q _v. Для реакций, протекающих с участием веществ в газообразном состоянии, в том числе идеальных и реальных газов при невысоких давлениях, к которым применимо уравнение Менделеева-Клапейрона,

,

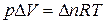т.е. при р, Т = const изменение объема вызвано уменьшением или увеличением числа моль газообразных! компонентов в системе:

.

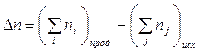Следовательно,

,

.

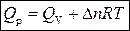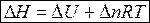3. Изотермический процесс (Т = const)

Рассмотрим изотермический процесс, протекающий в идеальном газе. Согласно закону Гей-Люссака-Джоуля внутренняя энергия идеального газа зависит только от температуры и не зависит от давления и объема. Это значит, что при
Т = const Δ U = 0. Это означает, что при Т = const внутренняя энергия идеального газа не изменяется, т.е. U = const, а dU = 0.

Следовательно,

.

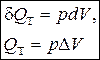Таким образом, в изотермическом процессе работа (d A = pdV) совершается только за счет поглощаемой теплоты (d Q _T).

Для идеального газа в соответствии с уравнением Менделеева Клапейрона

,

.

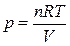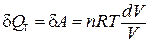После интегрирования

.

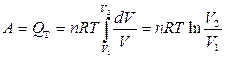При Т = const

,

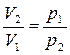тогда

.

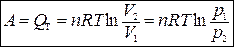4) Адиабатический процесс осуществляется без теплообмена с окружающей средой (d Q = 0).

.

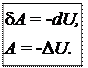В адиабатическом процессе работа может совершаться только за счет убыли внутренней энергии.

Таблица – Приложение I закона к термодинамическим процессам

Процесс	Уравнение I закона термодинамики	Уравнение для расчета работы расширения
Изохорный (V = const)	d Q v = dU, Q v = D U	p D V = 0
Изобарный (p = const)	d Q p = dH, Q p = D H	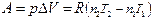, при p, T = const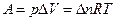
Изотермический (Т = const)	Для идеального газа
d Q T = pdV, Q T = p D V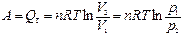
Адиабатический (Q = const)	d Q = 0	A = p D V = -D U

Дата добавления: 2014-01-07