Траектория точки

Траектория точки — это пространственная характеристика дви­жения: геометрическое место положений движущейся точки в рас­сматриваемой системе отсчета. На траектории определяют ее длину, кривизну и ориентацию в пространстве, а также перемещение точки.

Траектория — это непрерывная линия, воображаемый след движу­щейся точки¹: она дает пространственный рисунок движения точки (рис. 3). Расстояние по траектории показывает, каков путь точки²: [l] = L.

В прямолинейном движении (направление его не изменяется) (рис. 4) путь точки при движении в одну сторону равен расстоянию от начального положения до конечного. В криволинейном движении (направление его изменяется) путь точки равен расстоянию по тра­ектории в направлении движения от начального положения до конечного.

Кривизна траектории (к) показывает, какова форма движения точки в пространстве. Чтобы определить кривизну траектории, измеряют радиус кривизны (R). Кривизна — величина, обратная радиусу:

Если траектория является дугой окружности, то ее радиус кривизны постоянный. С увеличением кривизны ее радиус уменьша­ется, и наоборот, с уменьшением — увеличивается.

Ориентация траектории в пространстве при одной и той же ее форме может быть разная. Ориентацию для прямолинейной тра­ектории определяют по координатам точек начального и конечного положений; для криволинейной траектории — по координатам этих двух точек и третьей точки, не лежащей с ними на одной прямой линии.

Перемещение точки показывает, в каком направлении и на какое расстояние сместилась точка. Перемещение (линейное) находят по разности координат точки в моменты начала и окончания движения (в одной и той же системе отсчета расстояния):

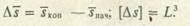
Перемещение определяет размах и направление движения. В случае, когда в результате движения точка вернулась в исходное положение,

1. След при движении оставляет точка, поэтому нужно говорить о траектории точки, а не движения.

2. Поскольку путь — это длина траектории, не следует говорить «длина пути».

3. Знак (греческая буква «дельта») обозначает приращение какой-либо величины.

перемещение, естественно, равно нулю. Перемещение — это не само движение, а лишь его окончательный результат, расстояние по пря-] мой и ее направление от начального до конечного положения.

Рассматривают элементарное перемещение (ds) точки — из данного положения в положение, бесконечно близкое к нему. Геометрическая сумма элементарных перемещений равна конечному! перемещению из начального положения в конечное. На криволинейной траектории элементарное перемещение считают равным пути.

Перемещение тела при поступательном и вращательном движении измеряется различно. Перемещение тела линейное (в поступа­тельном его движении) можно определить по линейному перемещению любой его точки. Ведь в поступательном движении прямая, соеди­няющая две любые точки тела, перемещаясь (прямолинейно либо криволинейно), остается параллельной своему начальному положению. Все точки "тела движутся одинаково: по подобным траекториям, с одинаковыми скоростями и ускорениями. Достаточно из координаты конечного положения любой точки тела вычесть соответствующую координату ее начального положения, чтобы определить перемещение всего тела.

Перемещение тела угловое (во вращательном его движении) определяют по углу поворота. При вращательном движении тела в нем имеется линия, все точки которой остаются во время всего движения неподвижными (лежат на оси). Остальные же точки тела движутся по дугам окружностей, центры которых лежат на этой неподвижной линии — оси вращения (рис. 4, в). Перемещение тела (угловое) находят по разности угловых координат условной линии отсчета (в одной и той же системе отсчета расстояния): дельта ф = ф_кон — ф_нач; [ф] = L°, где ф — угловая координата. Если из любой точки тела опустить перпендикуляр г на ось вращения г—z (см. рис. 4, в), то при вращении тела эта линия (радиус вращения) повер­нется в плоскости поворота вокруг оси на угол ф (угол поворота).

Рассматривают также элементарное угловое пере­мещение (dф) тела из данного углового положения в положение, бесконечно близкое к нему.

Любое движение тела в пространстве можно представить как геометрическую сумму его поступательного и вращательного (отно­сительно любого полюса, в частности его центра масс) движений¹.

Перемещение системы тел (биомеханической системы), из­меняющей свою конфигурацию, определить намного сложнее. В самых упрощенных случаях движение ее рассматривают как движение одной материальной точки — обычно общего центра масс (ОЦМ). Тогда можно проследить за перемещением всего тела человека «в целом», оценить в известной мере общий результат его двигательной дея­тельности. Но останется неизвестным, в результате каких именно движений достигнуто перемещение ОЦМ. Иногда перемещение тела человека представляют в виде перемещения условно связанной с ним линии (линия отсчета).

Изучение движений звеньев тела человека позволяет более подробно рассмотреть перемещение его тела. В некоторых случаях несколько подвижных частей (например, все кости стопы, кисти или предплечья, даже туловища) рассматриваются как одно звено — тогда уже можно в общих чертах уловить особенности движений, хотя взаимное дви­жение многих звеньев не учитывается и их деформациями пренебре­гают. Однако получить полную картину перемещений всех основных элементов тела (включая и внутренние органы, и жидкие ткани) при существующих методах исследования пока еще невозможно. В любом научном исследовании приходится прибегать к более или менее зна­чительному упрощению.

В машинах, характеризующихся определенностью движений, име­ется вполне определенный закон движений. В биомеханических систе­мах, характеризующихся неопределенностью движений в сочленениях, стараются добиваться требуемой определенности, но возможности

найти закон движения всех звеньев тела в целом очень невелики. Они несколько больше в видах спорта, где техническое мастерство проявляется (и в значительной мере) именно в точном воспроизведен заранее заданных, детально определенных движений (например, гимнастике, фигурном катании на коньках).

Дата добавления: 2014-01-07