Интегральная и дифференциальная форма закона полного тока

Количественная связь между циркуляцией вектора 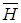по замкнутому контору и током внутри контура определяется законом полного тока в интегральной форме:

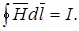(17.3)

Линейный интеграл от напряженности магнитного поля вдоль любого замкнутого контура равен полному току, пронизывающему замкнутый контур.

Интегральную форму закона полного тока применяют, когда может быть использована симметрия в поле. Определим напряженность поля в некоторой точке А в поле уединенного прямого провода с током I (рис. 17.3).

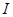
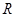
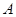
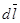
Рис. 17.3. к определению напряженности поля уединенного провода

Проведем через точку А окружность радиусом R в плоскости, перпендикулярной оси провода, так что центр ее находится на этой оси. В силу симметрии напряженность поля во всех точках окружности численно одна и та же. Направление напряженности совпадает с касательной к окружности:

;

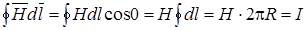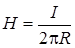. (17.4)

Если какое-либо поле имеет сложный характер и напряженность H нельзя вывести из-под знака интеграла, то использовать закон полного тока в интегральной форме так просто не удается.

Соотношение (17.3) пригодно для контура любых размеров, в том числе и для весьма малого.

Выделим в какой-либо среде небольшой контур и составим вдоль него циркуляцию вектора 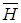(рис 13.4).

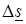
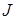
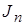
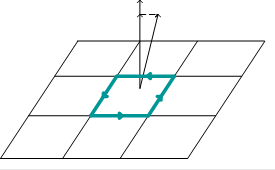
Рис. 17.4. К нахождению циркуляции вектора 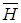для любого контура

Если площадь мала, то можно полагать, что плотность тока 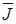в пределах этой площади одинакова, и тогда ток, пронизывающий площадь:

,

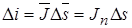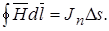
Разделим обе части равенства на Ds и устремим Ds к нулю. Возьмем предел полученного соотношения:

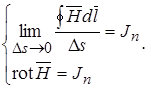
Если площадь 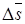ориентирована перпендикулярно к 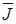, то

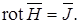(17.6)

Формула (17.6) называется законом полного тока в дифференциальной форме.

Ротор – это функция, характеризующая поле в рассматриваемой точке, в отношении способности к образованию вихрей. Раскрытие функции ротора в декартовой системе координат мы рассмотрели в параграфе 14.1.3 формулы (12.17), (12.18) и (12.19).

Дата добавления: 2014-01-07