Расчет магнитного поля одиночного проводника с током

Требуется рассчитать магнитное поле внутри и за пределами проводника (рис. 17.5). Это означает, что необходимо определить распределение напряженности и вектора-потенциала.

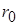
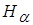
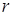
Рис. 17.5. К расчету магнитного поля одиночного проводника

Для расчета используем закон полного тока в интегральной форме

Рассчитаем циркуляцию вдоль окружности, центр которой совпадает с центром провода. При этом напряженность в любой точке этой окружности постоянна по модулю и совпадает с направлением элементарного участка dl.

Внутри проводника () .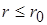

Следовательно, внутри проводника напряженность магнитного поля определяется выражением

.

Максимальное значение напряженности магнитного поля имеет место на поверхности проводника

Вне проводника (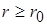) закон полного тока можно записать в виде 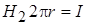. При этом распределение напряженности происходит по закону

.

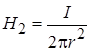Распределение напряженности магнитного поля внутри и вне проводника показано на рис. 17.6.

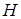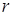
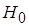
Рис. 17.6. Распределение магнитного поля одиночного проводника

Рассчитаем вектор-потенциал внутри проводника (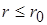). Так как по проводнику протекает ток, то вектор-потенциал подчиняется уравнению Пуассона .

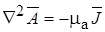Вектор-потенциал образует плоско параллельное поле, изменяющееся только по радиусу. Поэтому в цилиндрической системе координат уравнение Пуассона запишется

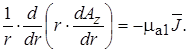(17.20)

Проинтегрировав его, получим

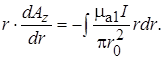(17.22)

Так как поблизости нет другого поля, то постоянную интегрирования C₁ можно приравнять к нулю. Тогда

.

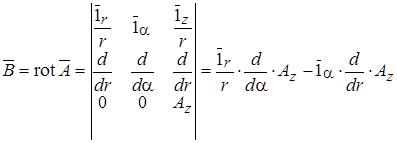В свою очередь,

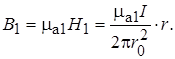(17.23)

При r = 0 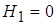, следовательно, и .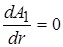

Проинтегрировав уравнение (17.21)*, получим

(17.24)

Если принять, что на поверхности проводника A₁ = 0, то постоянная интегрирования C₂ будет равна

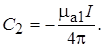
Тогда

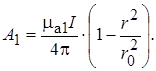(17.25)

Так как за пределами проводника тока нет, то вектор-потенциал подчиняется уравнению Лапласа .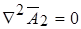

Используя то же допущение о плоско параллельном поле, получим

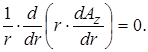(17.26)

На поверхности провода по закону полного тока

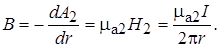(17.27)

Следовательно,

(17.28)

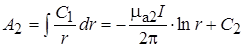(17.29)

Из условия непрерывности вектора-потенциала следует, что при 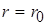A₂ = A₁ = 0.

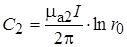(17.30)

Тогда

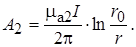(17.31)

Выделим в толще проводника элементарную площадку, нормаль к которой параллельна вектору напряженности (рис. 17.7).

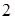
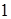
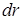
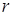
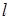
Рис. 17.7. К расчету вектора-потенциала магнитного поля

одиночного проводника с током

По теореме Стокса

(17.32)

Этот интеграл распадается на 4 составляющие

На участках 2-3 и 4-1 векторы 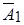и перпендикулярны, поэтому их скалярное произведение равно нулю.

Индуктивность, обусловленная магнитным потоком внутри проводника

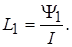
(17.33)

В свою очередь,

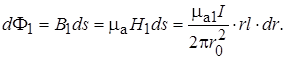(17.34)

Тогда

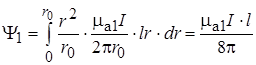; (17.35)

. (17.36)

За пределами проводника ()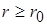

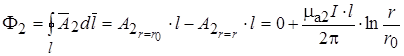
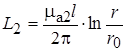(17.37)

Дата добавления: 2014-01-07