ЛЕКЦИЯ №2. Расчетная схема – это упрощенная схема реальной конструкции, в которой не учитываются второстепенные факторы

Расчетная схема

Расчетная схема – это упрощенная схема реальной конструкции, в которой не учитываются второстепенные факторы. Для передачи нагрузок конструкция должна быть зафиксирована относительно земли (фундамента).

В расчетной схеме пренебрегли: силой трения, конфигурацией опор, весом детали и т.д.

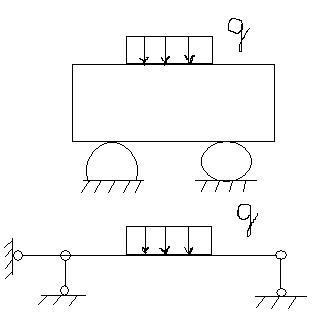Фиксирование осуществляется с помощью так называемых опор, воспринимающих внешние силы:

1) Жесткое защемление-заделка;

2) Шарнирно неподвижная опора;

3) Шарнирно подвижная опора.

Внутренние силы. Метод сечений.

Под действием внешних сил в теле возникают дополнительные внутренние силы взаимодействия между частицами материала. Сопромат изучает именно эти силы. В дальнейшем слово дополнительные будем опускать. Внутренние силы определяется методом сечений. Этот метод был введен немецкими инженерами Риттером и Шведлером в 19 веке.

Нарисуем деталь, находящуюся в равновесии

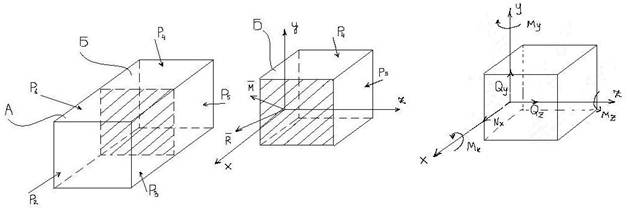
Для определения внутренних сил в произвольном сечении детали:

1. Р ассечем (мысленно) деталь по заданному сечению на две части;

2. О тбрасываем одну из частей, часть А;

3. З аменяем действие отброшенной части на оставшуюся внутренними силами, которые приводим в центр тяжести сечения в виде главного моментаи главного вектора .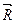

Удобно разложить главный вектор 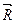и главный момент на составляющие относительно главных осей поперечного сечения:

N_X – продольная сила, вызывает растяжение (сжатие) детали;

Q_Y, Q_Z – поперечные силы, вызывают сдвиг детали;

M_Y, M_Z – изгибающие моменты, вызывают изгиб детали;

M_K – крутящий момент, вызывает закручивание детали.

4. У равновешиваем оставшуюся часть детали, используя уравнения статики (3 уравнения для сил, 3 уравнения для моментов)

Σ X = 0 ΣM_X = 0

Σ Y = 0 ΣM_Y = 0 6 уравнений статики

Σ Z = 0 ΣM_Z = 0

Для плоской системы тел – 3 уравнения статики. Из этих уравнений определяем величину внутренних сил.

Понятие о напряжениях

Метод сечений дает возможность определить внутренние силы, но не отвечает на вопрос, как распределены внутренние силы по сечению. Для измерения величины интенсивности внутренних сил служат напряжения.

Напряжение - это мера интенсивности внутренних сил в данной точке сечения.

Рассмотрим некоторое сечение тела и выделим элементарную площадку в окрестности точки В с площадью ΔА. По площадке действует сила ΔR. Здесь ΔR – равнодействующая внутренних сил на площадке ΔА.

Разложим силу ΔR на две составляющие:

ΔN – нормальная составляющая силы;

ΔT – касательная составляющая;

Следовательно р_СР = - полное среднее напряжение на площадке ΔА;

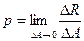- полное напряжение в точке В.

С полным напряжением действовать неудобно. Поэтому будем использовать следующие пределы отношения

- нормальное напряжение в точке В, действующее перпендикулярно сечению,

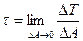- касательное напряжение в точке В, оно действует в плоскости сечения.

Связь между р, σ, 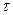: р =

Интегральные зависимости между усилиями и напряжениями

Получим эти соотношения, выделив элементарную площадку dA на поперечном сечении бруса. На этой площадке действуют нормальные σ и касательные 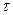напряжения. Разложим предварительно 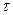на составляющие и . Площадь всего сечении бруса А. Таким образом, можно записать

,

, ,

, , .

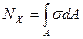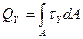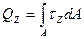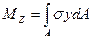Понятие о деформациях

Под действием нагрузки конструкция (деталь) деформируется, т.е. изменяется ее форма и размеры. Для определения деформации в точке А рассмотрим малый отрезок длинной S, исходящий из этой точки в произвольном направлении.

В результате деформации точка А сместится в положение А_1, а отрезок S удлинится на величину ΔS и измерит свое направление.

Предел отношения - носит название относительной линейной деформации в точке А по направлению АВ.

Аналогично определяются относительные линейные деформации в направлении осей X, Y, Z, следовательно, имеем ε_X, ε_Y, ε_Z.

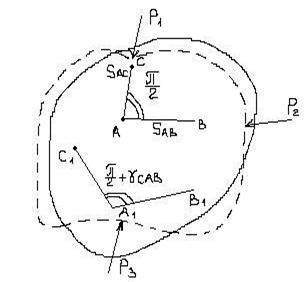Определим угловые деформации, нарисуем прямой угол ВАС. После деформации угол будет В₁А ₁С_1. Предел

- угловая деформация в точке A в плоскости ВАС.

Аналогично определяются угловые деформации в плоскости XY, XZ, YZ, следовательно, имеем , , .

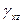Таким образом, в любой точке тела имеют место три линейных и три угловых компонента деформации, которые определяют деформированное состояние в точке.

Условие прочности

Определение условия прочности: максимальное напряжение, возникающее в элементах конструкций под действием внешних сил и не должно превышать допускаемых напряжений для материала, как по касательным, так и по нормальным напряжениям

σ_max ≤[σ], 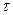_max≤[],

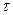σ_max, 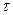_{max ,} - определяются расчетным путем, и берутся в опасном сечении, где действуют максимальные напряжения.

[σ], [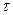] – допускаемые напряжения соответствуют принятому материалу и типу детали, а также определяется условиями и нормалями отрасли.

Такой метод оценки прочностной надежности называется методом расчета по допускаемому напряжению – наибольшему напряжению, при котором обеспечивается безопасная работа проектируемого элемента конструкций.

Для безопасной работы конструкции (детали) также ставится условие жесткости.

Определение условия жесткости: максимальные прогибы (углы закручивания) возникающие в элементах конструкций под действием внешних сил не должны превышать допускаемых прогибов (углов закручивания) для данной конструкции.

, ,

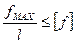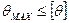ƒ_MAX и Ө_MAX – максимальный прогиб и максимальный угол закручивания для детали 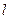– длина (пролет) балки. и 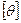допускаемый прогиб и угол закручивания определяется условиями и нормалями отрасли.

Дата добавления: 2014-01-07