Взаимно перпендикулярные прямые

Прямые скрещивающиеся

Прямые пересекающиеся

Относительное положение прямых

Проецирующие прямые

Прямые уровня

Комплексные чертежи прямых

Координатные фильтры

Ортогональное проецирование точки на плоскость

Построение исходных объектов

Первый этап решения задачи состоит в построении исходных объектов как примитивов AutoCAD’а по размерам, взятым с чертежа. Объектами могут быть точки, отрезки прямых, поверхности.

Исходный чертеж дан, как правило, в безосной форме. Необходимо на этом чертеже нанести оси декартовой системы координат (систему отсчета), относительно которой можно измерять координаты точек объектов. Направление осей нужно задать в соответствии с тем, которое принято в AutoCAD’е. Точка начала координат на чертеже может быть выбрана произвольно, поскольку она не влияет на разности координат точек, то есть не изменяет взаимного положения и формы заданных на чертеже объектов.

На рис. 14 дан чертеж треугольника АВС, содержащий его горизонтальную и фронтальную проекции. На поле чертежа нанесены оси координат. Координаты точек можно измерять линейкой с точностью до 1 мм. Так, координаты точки А равны (x = 10, y = 50, z = 22).

Построим точку А (см. рис. 14) как объект AutoCAD’а.

q Перейдите в окно вида сверху или в окно аксонометрии; в этих окнах система координат соответствует системе, нанесенной на чертеже.

q point \ 10, 50, 22.

q Результат: во всех видовых окнах появилось изображение точки в виде маркера – крестика.

Маркер, которым помечена точка, определен в прототипе. Можно изменить вид и размер маркера:

q Format (Режимы)\ Point Style (Отображение точек).

Построим отрезок прямой AC:

q line \ 10, 50, 22 \ 50,30,50.

Результат: отрезок построен. Он отображен во всех видовых окнах, следовательно, получены три его ортогональные проекции и аксонометрическая проекция (изометрия).

Для построения ортогональной проекции точки на плоскость, когда угол проецирования a=90⁰, (рис. 15) достаточно установить на эту плоскость систему координат (ПСК), определить координаты проецируемой точки в этой системе координат и приравнять нулю z-координату. Например, если ПСК установлена на плоскость D и точка А имеет в этой ПСК координаты (50,60,70), то ортогональная проекция точки А на плоскость D - это точка А_D (50,60,0).

Ортогональные проекции строят, применяя так называемые координатные фильтры - средство, позволяющее взять у указанной точки необходимые координаты. Так, если применить фильтр .xy, то у точки будут взяты только координаты x и y, а недостающую координату z система потребует задать дополнительно; для построения ортогональной проекции z-координату нужно задать равной нулю. Фильтры можно вызвать сочетанием клавиш Shift+ПЩ \ Point Filters (Фильтры).

Построим точку А_D, являющуюся ортогональной проекцией точки А на плоскость D (см. рис. 15):

q задайте маркер точки;

q установите ПСК в плоскость проекции D;

q point \ Shift+ПЩ \ Фильтры \.xy \ включите объектную привязку Shift+ПЩ \ Node (Узел);

q укажите прицелом проецируемую точку А;

q на запрос “требуется Z” введите ноль – точка А_D построена.

Проекцией отрезка также будет отрезок, для построения которого нужно взять точки проецируемого отрезка, применив координатный фильтр.xy и объектную привязку Endpoint (Конечная). Пусть имеется отрезок; нужно построить его ортогональную проекцию в заданную плоскость:

q установить ПСК в плоскость проецирования.

q line \ выберите фильтр (Shift+ПЩ \ Фильтры \.xy);

q включите объектную привязку (Shift+ПЩ \ Конечная) \ укажите конец проецируемого отрезка \ на запрос “требуется z” введите ноль;

q повторите те же действия для второй конечной точки отрезка \ ПЩ – проекция отрезка построена.

2.3.2. “Автоматическое” проецирование

Проецирование можно “поручить” системе, применив программу project.lsp, которую нужно предварительно загрузить[1].

q Загрузите файл project.lsp (Tools \ Load Application...)

Результат: загруженная программа создает три новые команды: ПРОЕКЦИЯ, ПР1, ПР2.

q Введите команду ПРОЕКЦИЯ (PROJECT) и прочтите информацию о пользовании программой.

Команда ПР1 осуществляет ортогональное проецирование объектов в плоскость ПСК. Объектами могут быть точки, отрезки прямых и дуги окружности, полилинии. Команда ПР2 осуществляет косоугольное проецирование, о нем см. ниже. Для выполнения ортогонального проецирования:

q установите ПСК в плоскость проецирования;

q введите команду ПР1 и укажите объекты для проецирования \ ПЩ.

Результат: получены ортогональные проекции выбранных объектов на плоскость ПСК.

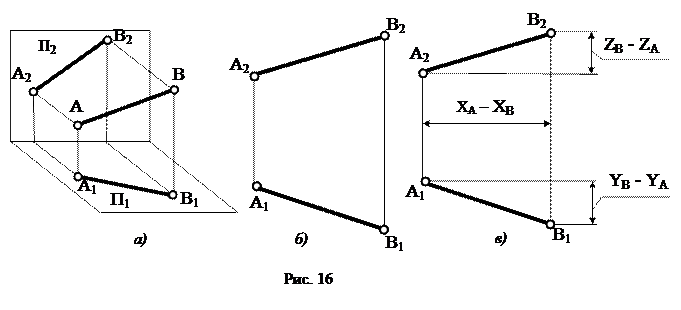
Так как прямая определяется двумя точками, то для задания ее на чертеже доста­точно проекций двух принадлежащих ей точек (рис. 16, а, б).

При безосном способе изображения расстояние между проекциями берется произ­вольно, но обязательно соблюдается разница координат точек, задающих прямую, (рис. 16, в).

Прямая может занимать различные положения в пространстве относительно плоскостей проекций. Прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций называется прямой общего положения (рис. 16). Остальные прямые относят к прямым частного положения, среди которых различают прямые уровня и проецирующие прямые. Прямые уровня – это прямые параллельные одной из плоскостей проекций, проецирующие прямые – прямые перпендикулярные плоскостям проекций.

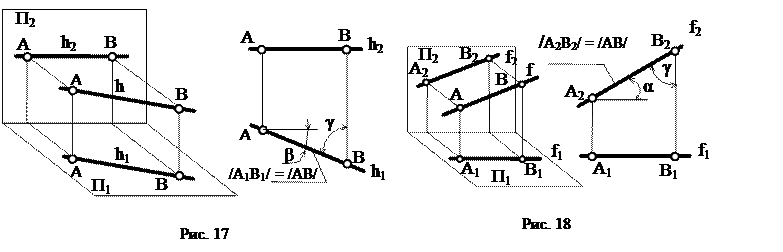
Прямая уровня, параллельная горизонтальной плоскости проекций, называется горизонталью (рис. 17), прямая, параллельная фронтальной плоскости проекций – фронталью (рис. 18) и прямая, параллельная профильной плоскости проекций, носит название профильной прямой (рис. 19).

Горизонталь обозначают буквой h. Ее фронтальная проекция h₂ всегда перпендикулярна вертикальным линиям связи, а горизонтальная проекция h₁ отражает положение прямой в пространстве. Отрезок /AB/ и углы наклона β, γ к плоскостям проекций П₂ , П₃ проецируются на плоскость П₁ без искажения.

Фронталь обозначают буквой f. У фронтали всегда перпендикулярна линиям связи горизонтальная проекция f₁, а фронтальная проекция f₂ соответствует положению самой прямой в пространстве. Углы наклона α и γ к плоскостям П₁ и П₃ соответственно, а также отрезок /АБ/ фронтали, проецируются на П₂ без искажения.

Профильную прямую обозначают буквой p. Ее фронтальная p₂ и горизонтальная p₁ проекции совпадают с одной вертикальной линией связи, а профильная проекция p₃ отображает положение прямой в пространстве. Без искажения проецируются на П₃ отрезок /AB/ и углы наклона α, β профильной прямой к плоскостям П₁ и П₂ соответственно.

В зависимости от перпендикулярности к той или иной плоскости проекций прямые называют горизонтально, фронтально или профильно проецирующие.

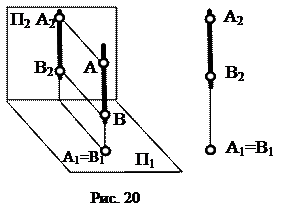Горизонтально проецирующая прямая – прямая, перпендикулярная П₁ (рис. 20). Горизонтальная проекция этой прямой (А₁=В₁) вырождается в точку, а фронтальная проекция (А₂В₂) совпадает с линией связи. Очевидно, что горизонтально проецирующая прямая одновременно параллельна П₂ и П₃, следовательно, /A₂B₂/ = /A₃B₃/ = /AB/.

Фронтально проецирующая прямая – прямая перпендикулярная П₂ (рис. 21). Фронтальная проекция этой прямой (А₂=В₂) вырождается в точку, а горизонтальная проекция (А₁В₁) совпадает с линией связи. Фронтально проецирующая прямая параллельна П₁ и П₃, следовательно, /A₁B₁/ = /A₃B₃/ = /AB/.

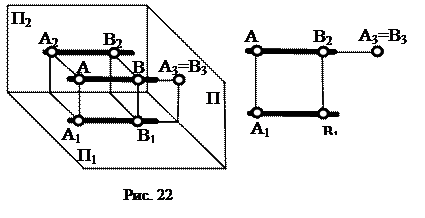
Профильно проецирующая прямая – прямая перпендикулярная П₃ (рис. 22). Профильная проекция такой прямой (А₃=В₃) представляет собой точку, а горизонтальная и фронтальная проекции перпендикулярны линиям связи. Профильно проецирующая прямая одновременно параллельна П₁ и П₂, следовательно, /A₁B₁/ = /A₂B₂/ = /AB/.

Точки, принадлежащие проецирующей прямой, называют конкурирующими относительно плоскости проекций, которой перпендикулярна прямая. Точки А и В на рис. 20 называются горизонтально конкурирующие, на рис. 21 и 22 соответственно фронтально и профильно конкурирующие. Конкурирующие точки применяются для определения видимости проекций геометрических фигур.

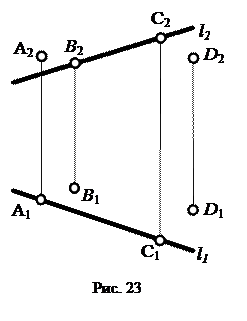2.4.3. Принадлежность точки прямой линии

Точка может принадлежать прямой или находиться вне ее. Если точка принадлежит прямой, то все проекции данной точки должны принадлежать одноименным проекциям прямой (рис. 23).

Например, точка С принадлежит прямой l, так как С₁ и С₂ принадлежат соответственно l₁ и l₂.

Точка не принадлежит прямой, если хотя бы одна ее проекция не принадлежит одноименной проекции прямой. Например, точки А, В, D не принадлежат прямой l, причем точка А расположена над прямой, а точка В за прямой.

Определение длины отрезка прямой способом прямоугольного треугольника

Так как прямая общего положения не параллельна ни одной из плоскостей проекций, то отрезок, ей принадлежащий, проецируется на данные плоскости с искажением.

Рассмотрим прямоугольный треугольник АВВ₀ (рис. 24, а). Гипотенуза АВ треугольника есть сам отрезок в пространстве, катет В₀В равен горизонтальной проекции отрезка А₁В₁, а катет АВ₀ представляет собой разницу высот концов отрезка Z_A - Z_B до плоскости проекций П_1. Угол α является углом наклона отрезка к П₁. Треугольник, равный данному, можно построить на комплексном чертеже (рис. 24, б). Используя в качестве катета горизонтальную проекцию отрезка А₁В₁, строим второй катет, равный разнице высот Z_A – Z_B, которую определяем по фронтальной проекции отрезка А₂В₂. Гипотенуза В₁В₀ равна натуральной величине отрезка /AB/, угол α – угол наклона отрезка к П₁. Длина отрезка может быть определена также как длина гипотенузы прямоугольного треугольника, одним катетом которого является фронтальная проекция А₂В₂, а другим - разница координат Y_B – Y_A, которую определяем по горизонтальной проекции отрезка (рис. 24, в). Угол β в данном случае будет равен углу наклона отрезка к фронтальной плоскости проекций П₂.

Таким образом, если требуется определить истинную величину отрезка прямой и угол его наклона к плоскости П₁, прямоугольный треугольник строят, используя горизонтальную проекцию отрезка. Если требуется истинная величина и угол наклона к П₂ – используется фронтальная проекция.

Две прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися.

Прямые параллельные

Если прямые а, б параллельны, то их проекции также параллельны (рис. 25, а). Справедливо и обратное утверждение, но только для прямых общего положения.

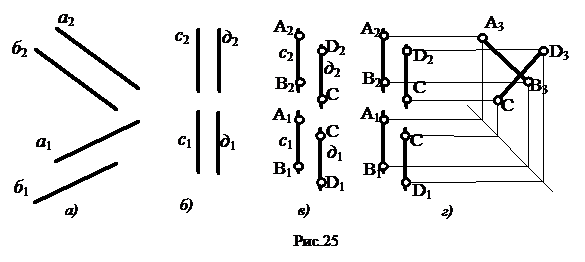
Таким образом, чтобы судить о параллельности двух прямых общего положения, достаточно иметь две любые их проекции. В случае прямых уровня не всегда по двум проекциям можно определить их параллельность. Например, на рис. 25, б взаимное положение профильных прямых вообще не определено. Для однозначного задания таких прямых, с использованием тех же проекций, необходимо указать проекции точек A,B,C,D, принадлежащих им (рис. 25, в). Однако судить о параллельности прямых с и d на рис. 25, в весьма затруднительно. Другое дело, если имеются проекции профильных прямых на плоскость, которой они параллельны (рис. 25, г). Как видно из рис. 25, г проекции А₃В₃ и С₃В₃ не параллельны, следовательно, прямые в пространстве не параллельны.

Таким образом, чтобы судить о параллельности прямых уровня необходимо иметь их проекции на плоскость, которой они параллельны.

Если прямые пересекаются в пространстве, то их проекции тоже пересекаются и точки пересечения проекций К₁, К₂ принадлежат одной линии связи (рис. 26, а).

Проекции скрещивающихся прямых m, n могут пересекаться (рис. 26, б), однако точки пересечения проекций не принадлежат одной линии связи. Точка пересечения горизонтальных проекций скрещивающихся прямых m и n является горизонтальной проекцией двух горизонтально конкурирующих точек 1 и 2. Точка пересечения фронтальных проекций этих прямых является фронтальной проекцией фронтально конкурирующих точек 3, 4.

По горизонтально конкурирующим точкам определяют положение скрещивающихся прямых относительно горизонтальной плоскости проекций. Фронтальная проекция 1₂ точки 1, принадлежащей m, находится выше, чем 2₂ – точки 2, принадлежащей n (направление взгляда показано стрелкой). Следовательно, в данном месте прямая m над прямой n.

По фронтально конкурирующим точкам определяют положение скрещивающихся прямых относительно фронтальной плоскости проекций. Горизонтальная проекция 4₁ точки 4, принадлежащей m, расположена ниже, чем 3₁ – точки 3, принадлежащей n (направление взгляда показано стрелкой). Следовательно, прямая m расположена перед прямой n.

Любой угол между прямыми отображается на плоскость проекций без искажения, если прямые параллельны данной плоскости, т.е. являются прямыми уровня.

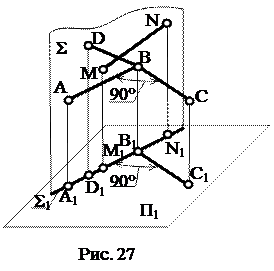
Особыми свойствами обладает прямой угол при ортогональном проецировании. Прямой угол проецируется без искажения, если только одна из его сторон параллельна плоскости проекций.

Для доказательства данного утверждения рассмотрим рис. 27. Дан прямой угол АВС, стороны которого АВ и ВС параллельны плоскости П₁. Следовательно, согласно свойствам параллельного проецирования, угол А₁В₁С₁ – проекция угла АВС, также прямой угол. ВС _┴ АВ и ВВ₁ по условию и по построению соответственно, отсюда ВС _┴ Σ – плоскости, проведенной через АВ и А₁В₁ и _┴ П₁. Как известно из школьного курса геометрии, если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей данной плоскости. Следовательно, ВС _┴ ВD и MN, и, соответственно, В₁С_{1 ┴} B₁D₁ и M₁N₁.

На комплексном чертеже возможны следующие случаи задания прямого угла: прямой общего положения а и горизонталью h (рис. 28, а), прямой общего положения в и фронталью f (рис. 28, б), прямой общего положения с и профильной прямой р (рис. 28, в).

В общем случае, когда стороны прямого угла являются прямыми общего положения, прямой угол проецируется с искажением, в острый или тупой угол.

Дата добавления: 2014-01-07