Эквивалентные функции. Контрольні запитання

СРАВНЕНИЕ ФУНКЦИЙ

Лекция 2.3

Теми рефератів

Контрольні запитання

До ПЗ 4.

1. Які ознаки є основою класифікації системи «людина – машина»?

2. За якими принципами розподіляються функції системи «людина – машина» і які вимоги при цьому висуваються?

3. Які інженерно-психологічні властивості?

4. Як здійснюється передавання інформації системи «людина – машина»?

5. Охарактеризуйте інформаційну і концептуальну моделі діяльності оператора в системі «людина – машина».

1. Психологічні основи класифікації системи «людина – машина».

2. Інженерно-психологічні основи розподілу функцій у системі «людина – машина».

3. Інженерно-психологічні характеристики функціонування системи «людина – машина».

4. Роль концептуальних моделей у процесі управління системи «людина – машина».

ОПРЕДЕЛЕНИЕ 1. Пусть функции f (x), g (x) определены в некоторой проколотой окрестности точки а и отличны от нуля во всех точках этой окрестности. Эти функции называются эквивалентными (асимптотически равными) при х ® а, если

.

ПРИМЕРЫ.

1)sin x ~ x при х ® 0;

2) ~ x ² при х ® ¥.

Если сравниваемые функции обе бесконечно малые или бесконечно большие при х ® а, то их эквивалентность означает, что скорость их стремления к нулю или к бесконечности одинакова.

Пусть a(х) – бесконечно малая при х ® а функция. Тогда при х ® а

· sin(a(х)) ~ a(х)

· arcin(a(х)) ~ a(х)

· arctg(a(х)) ~ a(х)

· tg(a(х)) ~ a(х)

· 1 – cos(a(х)) ~ a²(х)/2

· ln(1+a(х)) ~ a(х)

· e^{a( х )} – 1 ~ a(х)

· sh(a(х)) ~ a(х)

· (1 + a(х)) ^k – 1 ~ k a(х)

ПРИМЕР.

tg(х– 1) ~ х– 1 при х ® 1.

ТЕОРЕМА 1. (Замена функций на эквивалентные при вычислении предела.)

Пусть f (x) ~ f ₁(x), g (x) ~ g ₁(x) при х ® а. Тогда, если существует 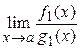, то существует и , причем

= .

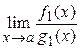Доказательство.

= =

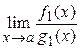
Последнее преобразование правомерно, так как обе функции отличны от нуля в проколотой окрестности точки а.

Поскольку обе части равенства равноправны, то предел, стоящий в левой части равенства, существует тогда и только тогда, когда существует предел, стоящий в правой части.

ПРИМЕРЫ.

1) =.

2) = = = .

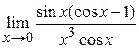Если бы мы формально заменили функции, стоящие в числителе дроби, на эквивалентные, то получили бы следующий результат:

==.

Итак, в случае суммы или разности функций замену их на эквивалентные при вычислении предела производить нельзя!!!

Дата добавления: 2014-01-07